编译原理笔记 6

目标代码生成及代码优化基础

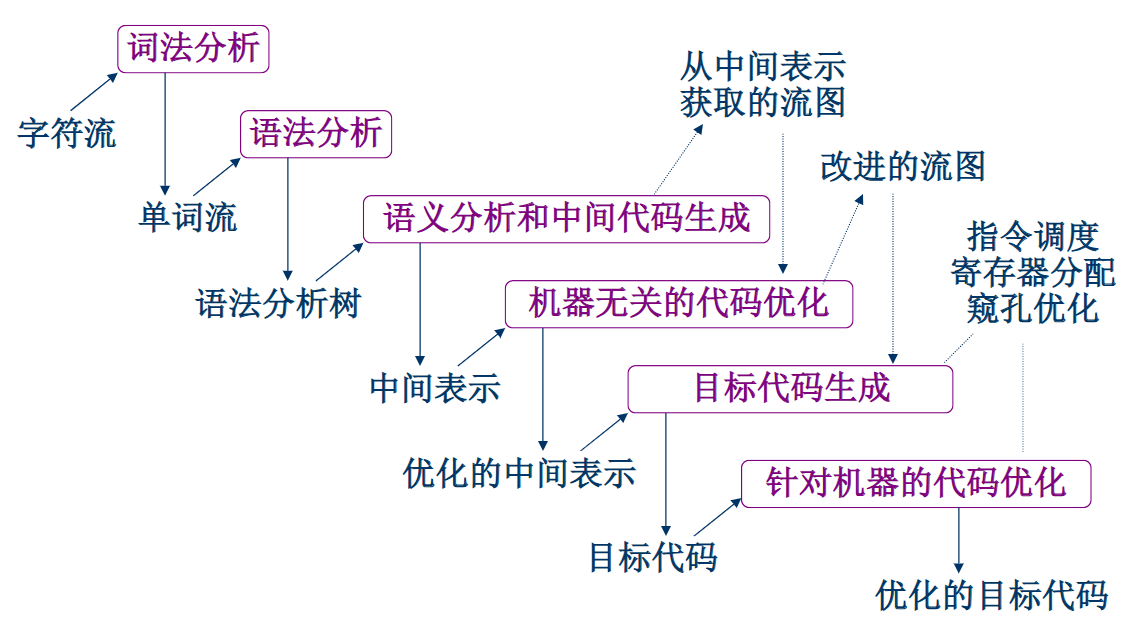
编译器整体逻辑

基本概念

基本块

对应实验中的：basicblock

一个顺序执行的语句序列，只有一个入口和一个出口，只有入口可能是label，只有出口可能是跳转或halt语句，具体来说：

入口可能是：
- 整个程序的第一条语句
- 某条跳转语句的目标
- 紧跟条件跳转语句的语句
出口可能是：
- 跳转语句
- halt
- 其他

划分基本块算法：

求出所有入口语句
由入口语句构造对应基本块：
- 到下一入口（不包含）
- 到跳转或halt（包含）

之后，不在基本块的语句都是不可到达的

流图

对应实验中的：cfg

表示程序的控制流信息，以基本块为点集，节点0一定是含有首条语句的基本块，存在有向边i -> j当且仅当：

i的出口是跳到j的入口
i的出口不是无条件跳转或停并且j紧跟i

循环

首先定义支配节点：

如果去除节点m后，从首节点出发不能到达节点n，则称m是n的支配节点，即为m DOM n，节点n的所有支配节点集合成为支配节点集，即为D(n)

之后定义回边：

对于一条有向边n -> d，其为回边当且仅当d DOM n

每一个回边n -> d对应一个自然循环为下面这些点构成的集合：

n和d
去除d后仍可到达n的节点

数据流分析基础

常用的手段是建立和求解数据流方程，例如：

\mathrm{out}(S) = \mathrm{gen}(S) \cup (\mathrm{in}(S) - \mathrm{kill}(S))

到达-定值数据流分析

对于变量A的定值是指一条TAC语句赋值或可能赋值给A，最普通的例如直接对A赋值或读值到A，这种语句的位置成为A的定值点

如果变量A的定值点d可以到达另一点p，要求d -》 p连通且路径上没有其他定值

对于基本块 $B$ ，我们定义：

$P[B]$ 为 $B$ 的所有前驱
$\mathrm{GEN}[B]$ 为B中定值并且到达了出口处的定值点集合
$\mathrm{KILL}[B]$ 为到达B入口、其定值的变量在B内被重新定值的定值点集合
$\mathrm{IN}[B]$ 为B入口处各变量所有定值点的集合
$\mathrm{OUT}[B]$ 为B出口处各变量所有定值点的集合

则其数据流方程为：

\begin{align*} \mathrm{IN}[B] &= \mathop{\cup}\limits_{b\in P[B]} \mathrm{OUT}[B] \\ \mathrm{OUT}[B] &= \mathrm{GEN}[B] \cup (\mathrm{IN}[B] - \mathrm{KILL}[B]) \end{align*}

计算的算法为：

$\mathrm{IN}[B_{i}] = \empty$ ， $\mathrm{OUT}[B_{i}] = \mathrm{GEN}[B_{i}]$
循环使用上述方程计算直到 $\mathrm{IN}[B]$ 保持稳定

到达定值数据流为一种典型的向前流，即信息流和控制流同向

活跃变量数据流分析

对应实验中的：livenessanalyzer

变量A在点p活跃表示存在从p开始的某条通路需要引用A在p处的值

对于基本块 $B$ ，我们定义：

$P[B]$ 为 $B$ 的所有后继
$\mathrm{LiveUse}[B]$ 为B中定值前要引用的变量集合
$\mathrm{Def}[B]$ 为B中定值、且定值前未被引用的变量集合
$\mathrm{LiveIn}[B]$ 为B入口处活跃变量的集合
$\mathrm{LiveOut}[B]$ 为B出口处活跃变量的集合

\begin{align*} \mathrm{LiveIn}[B] &= \mathrm{LiveUse}[B] \cup (\mathrm{LiveOut}[B] - \mathrm{Def}[B])\\ \mathrm{LiveOut}[B] &= \mathop{\cup}\limits_{s\in S[B]} \mathrm{LiveIn}[s] \end{align*}

计算的算法为：

$\mathrm{LiveIn}[B_{i}] = \mathrm{LiveUse}[B_{i}]$ ， $\mathrm{LiveOut}[B_{i}] = \empty$
循环使用上述方程计算直到 $\mathrm{LiveOut}[B]$ 保持稳定

活跃变量数据流为一种典型的向后流，即信息流和控制流反向

UD链和DU链

变量A在点u处的引用定值链（UD链）是指到达u的A的定值点全体，算法为：

如果A在基本块中被定值，定值点为d，且d在u之前，则A在u的UD链就是[d]
如果A在基本块中的u点之前没有被定值，A在u的UD链就是IN[B]

变量A在定值点u处的定值引用链（DU链）是指u处对变量A定的值被使用的引用点全体

DU链的一种算法为扩充活跃变量数据流：

$\mathrm{LiveUse}[B]$ 为(s, A)的集合，其中s在 $B$ 中且引用了A，并且s之前没有给A定值
$\mathrm{Def}[B]$ 为(s, A)的集合，其中s不在 $B$ 中且引用了A，并且A在B中被重新定值

待用信息与活跃信息

待用信息：基本块内某定值点下一次被使用的地方
活跃信息：基本块中的活跃信息链体现了以语句为单位的活跃变量信息，即如果i定值A、j引用A、i -> j之间没有重新定值，则i -> j之间A是活跃的

算法为倒序扫描，对于每一个 $A = B \,\mathrm{op}\, C$ ：

A 非待用，非活跃
B和C 待用信息为i，活跃

基本块的DAG

有向无圈图，叶节点代表名字初值，内部节点由运算符号标记

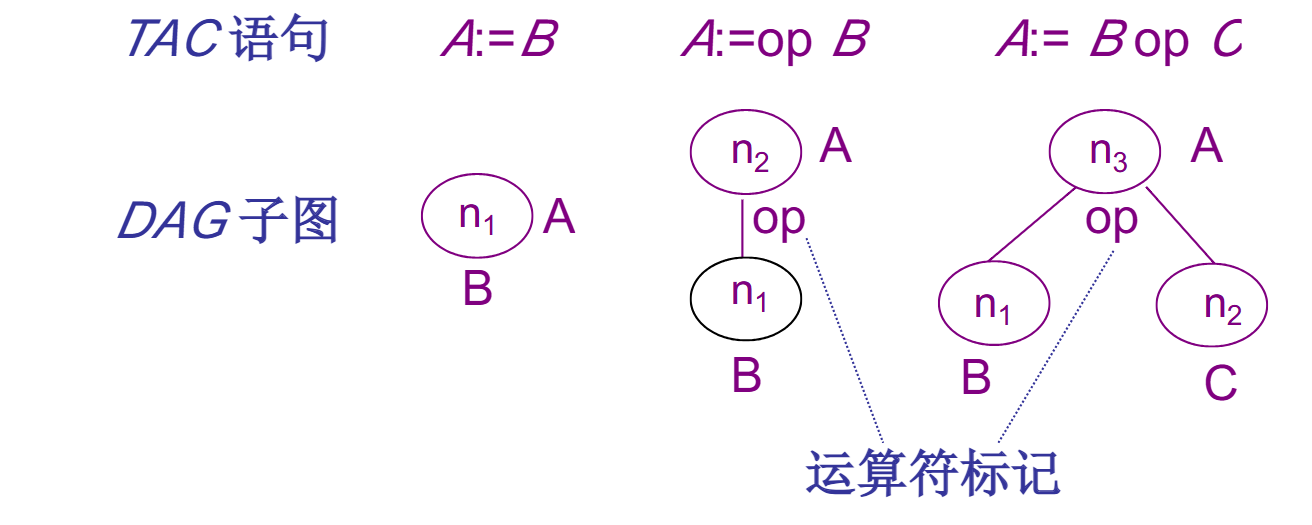
基本块的DAG

DAG生成算法大概就是：

常数直接生成（包括可以计算出的常数）
动态计算按照图中规则生成
尽可能复用
很简单！（不是我懒得抄）

可以使用DAG优化基本块

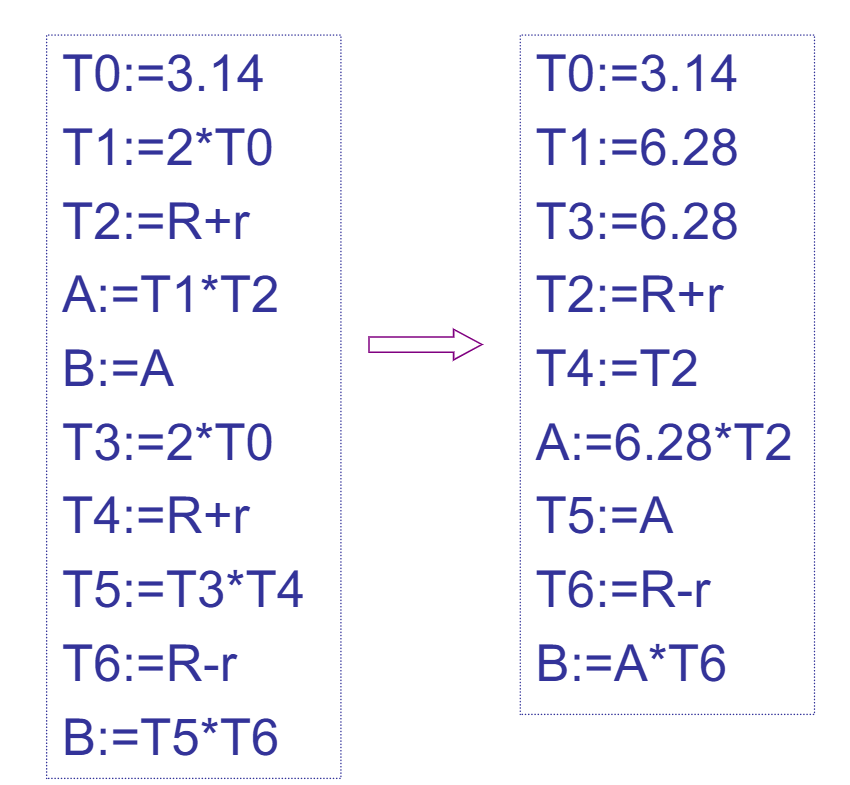
基本块优化DAG

目标代码生成

目标代码生成需要考虑：

指令选择：优先保证语义一致性，之后考虑效率
寄存器分配
指令调度

高效使用寄存器

Ershov数代表表达式求值时所需要寄存器数目的最小值，计算算法为：

def ershov(tree):
  for node in tree.backwardIterator():
    if node.ls is None and node.rs is None:
      node.ershov = 1
    elif node.rs is None:
      node.ershov = node.ls.ershov
    elif node.ls.ershov == node.rs.ershov:
      node.ershov = node.ls.ershov + 1
    else:
      node.ershov = max(node.ls.ershov, node.rs.ershov)

即：

叶节点的ershov数为1
如果只有一个孩子，则为孩子的ershov
如果左右儿子的ershov相同，则取孩子的ershov+1
如果左右儿子的ershov不同，则取较大者

表达式树的求值使用Sethi-Ullman算法，一种简略的算法为先递归计算孩子中ershov数更大的子树

两遍的寄存器分配和指派算法（实验框架中的做法）：

第一次分配给通用寄存器
第二次将通用寄存器绑定到物理寄存器

图分配算法

基于寄存器相干图的图着色寄存器分配算法

寄存器相干图定义为：

节点为伪寄存器
如果在某条语句中，节点i被定值，节点j是活跃的，则i, j之间有一条边

语句的活跃变量集合可以倒序遍历语句得到，算法为：

1
2
3

live = bb.liveOut
for instr in bb.instrs[::-1]:
    instr.live = live - instr.def + instr.use

之后用 $k$ （ $k$ 为物理寄存器数目）种颜色对相干图进行着色即可，但是k着色是一个NPC问题，因此有一种简单的启发式算法：

依次删除所有度小于 $k$ 的节点，这些点满足：我们可以在分配完其所有邻居之后为其分配一个新颜色
如果能到达空图，则代表可以k着色，反之不可以k着色，这代表我们需要把一个节点放到内存中（删除之），再继续分配

代码优化技术

按照优化范围分
- 窥孔优化：几条指令
- 局部优化：基本块
- 全局优化：流图
- 过程间：程序
按照对象分
- 目标代码优化
- 中间代码优化
- 源级优化
按照优化方式分
- 指令调度
- 寄存器分配
- 存储层次优化
- 存储布局优化
- 循环优化
- 控制流优化
- 过程优化等

窥孔优化

在目标指令序列上滑动一个包含若干条指令的窗口（即窥孔），如果发现不好的指令序列则优化

删除冗余内存操作
合并已知量
常量传播（可能使得更多的指令不可达从而被删除）
代数化简（删除x = x + 0这种）
控制流优化（减少跳转次数）
死代码删除（if(false) ...）
强度削弱（乘法变加法，除法变乘法或移位）
使用目标机惯用指令

循环优化

外提循环不变量，即循环中不变的代码可能可以放到循环外，可以利用UD来判断

循环不变量的外提

对于归纳变量（在每一次迭代都有新值的变量，例如循环下标），可以削弱计算强度，删除冗余归纳变量

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。