编译原理 笔记 3

语法制导的语义计算基础

以上下文无关文法为基础，有两种分类：

• 属性文法：侧重语义计算规则
• 翻译模式：侧重语义计算过程

属性文法

基于CFG的改进：

• 为每个文法符号关联多个属性（类的成员）
• 为每个产生式关联一个语义规则集合（或称为语义动作）

语义动作就是使用当前产生式的时候，需要调用某个函数，或需要对产生式中出现的某个文法符号的某个属性进行赋值
如果产生式$A\to \alpha$关联了语义规则$b\coloneqq f(c_{1}, \dots, c_{k})$

• 如果$b$是$A$的属性，则称$b$是$A$的综合属性
• 如果$b$是$B\in\alpha$的属性，则称$b$是$B$的继承属性

基于属性文法的语义计算

计算方法分为两类：

• 树遍历方法
• 单遍的方法

基于树遍历方法的语义计算

1. 构造输入串的语法分析树
2. 构造依赖图
3. 如果依赖图无圈，则可以按照该图的任何一种拓扑排序（排序中不改变有向边的关系）计算所有属性值
4. 如果依赖图有圈，则不可以按照这种方法进行计算

依赖图的构造需要遍历两遍分析树，按照如下方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

graph = DependencyGraph()
for node in tree.internal_nodes:
    # create nodes for all attributes of this non-terminator
    graph.create_nodes(node.productions.attributes) 
    # create nodes for those functions instead of an assignment
    graph.create_nodes(node.productions.functions, virtual==True)
for node in tree.internal_nodes:
    for rule in node.productions:
        # the vertex on behalf of this production
        vertex = rule.vertex
        parameters = rule.rhs.parameters 
                     if isinstance(rule, Assignment)
                     else rule.parameters
        for para in parameters:
            graph.add_edge(vertex, para.vertex)

在计算完成后，我们可以得到一个完整的、已知每个节点的所有属性值的语法分析树，这棵树被称为带标注的语法分析树

基于单遍方法的语义计算

可以看出，树遍历分析需要遍历两次语法分析树，并且会有非良定义的情况，因此提出另一种基于单遍的方法，分为自下而上和自上而下两种，只适用于特定的两类文法，我们讨论两种：

• S-属性文法：只包含综合属性
• L-属性文法：对于产生式右端的任意符号，其继承属性的计算只依赖于其左边符号的属性，因此如果涉及到产生式左端文法符号，则只能是继承属性

S-属性文法的语义计算

通常采用自下而上的方法进行

如果采用LR分析方法，则多加一个语义栈，存放综合属性的值

由于S-属性文法只包含有综合属性，因此在需要通过产生式来规约的时候，产生式右端的各个符号所包含的，出现在该产生式所关联的语义规则右端的属性值，应当已经计算完成

利用LR分析进行S-属性文法语义计算的例子

L-属性文法的语义计算

采用DFS后序遍历的方法进行，首先遍历每一个产生式右端所需要的参数，计算其值之后再计算左端的值

利用LL分析进行L-属性文法语义计算的例子

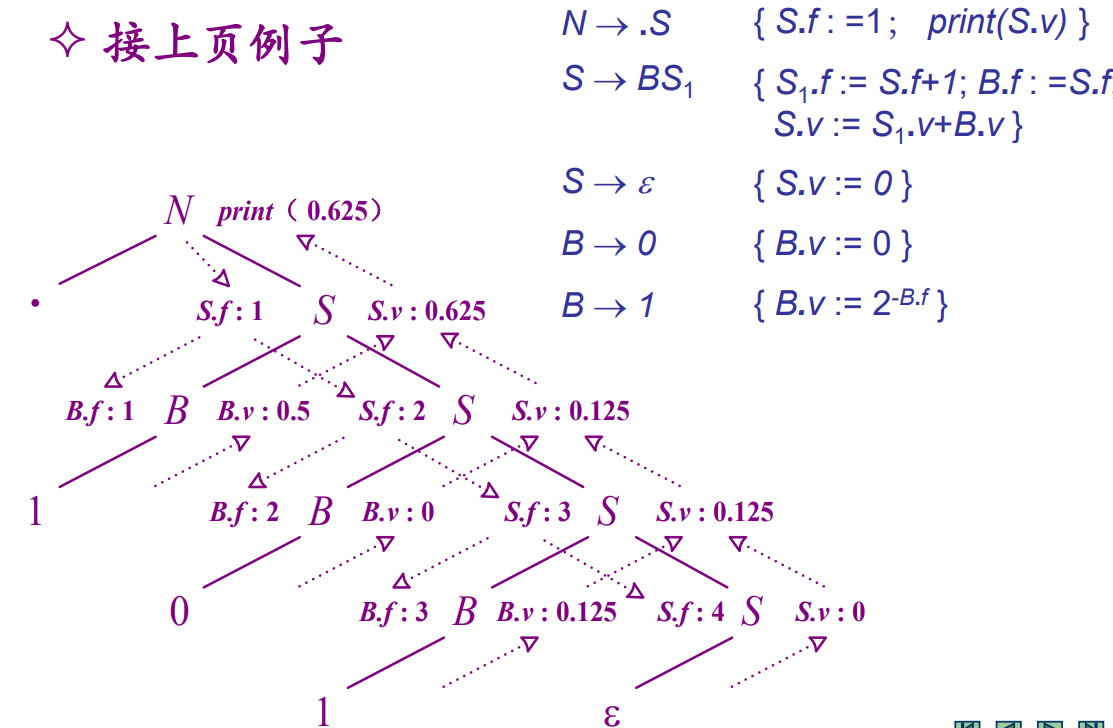
基于翻译模式的语义计算

与基于属性文法的语义计算类似，但是允许语义规则集合出现在产生式右端的任何位置，显式地表示动作和属性计算的次序

因此我们需要限制每个属性值在被访问到的时候已经存在：

• 类S-属性文法：仅包含综合属性的情形，直接将语义规则集合放在产生式右端的末尾即可
• 类L-属性文法：右端符号的继承属性的计算必须位于该符号之前，并且其只能依赖于产生式左边符号的属性；计算产生式左端非终结符相应的语义规则置于产生式的尾部

翻译模式文法举例

我们只使用单遍的方法

自上而下

处理比较简单，在每一个ParseX函数中，将对应的语义规则集合加入到合适的位置即可，注意此时ParseX函数可能有参数了，参数即为X的继承属性

如果原来文法含有左递归，则需要在消除左递归的同时对翻译模式中的语义规则进行变换，变换方式为：

将：

$$\begin{align*} A &\to A_{1}Y\{A.a \coloneqq g(A_{1}.a, Y.y)\} \\ A &\to X\{A.a \coloneqq f(X.x)\} \end{align*}$$

变为：

$$\begin{align*} A &\to X\{R.i \coloneqq f(X.x)\}R\{A.a \coloneqq R.s\} \\ R &\to Y\{R_{1}.i \coloneqq g(R.i, Y.y)\}R_{1}\{R.s\coloneqq R_{1}.s\} \\ R &\to \varepsilon\{R.s\coloneqq R.i\} \end{align*}$$

可以理解为，$R$的综合属性$R.i$用于计算，代替了原文法中$A.a$的作用，但是由于我们的计算现在是递归进行但是文法没有递归，所以我们需要增加一个继承属性$R.s$用于从下往上传递信息

详情请参考：

自下而上

类S-属性文法的计算是相似的，核心是类L-属性文法的自下而上计算（非常复杂，仅做简介）

• 从翻译模式中去掉嵌在产生式中间的语义规则集：
  • 若规则集合中未关联任何属性，则引入新终结符$N$与$N\to \varepsilon\{\cdots\}$，后方跟随规则集合
  • 若规则集合中关联了一些属性，则引入新终结符$N$与$N\to \varepsilon\{\cdots\}$，后方跟随规则集合，并在适当的地方增加复写规则
• 继承属性的访问：产生式右端的符号串中，靠左符号的综合属性可以替代靠右符号的继承属性
  • 例如$A\to XY$中，如果关联的语义规则需要用到继承属性$Y.i$，并且存在复写规则$Y.i\coloneqq X.s$则可以用$X$的综合属性$X.s$来代替
  • TODO
    详情请参考：

（皂基导致的，可不是我懒噢）