计算机网络安全技术 笔记 2

消息验证

在网络中，攻击手段包括：

  • 伪装：攻击者产生非法信息或欺诈应答
  • 内容修改：修改内容
  • 顺序修改：对双方发送消息的顺序进行修改
  • 计时修改：对消息的延时和重放
  • 发送方否认：发送方否认发送过消息
  • 接收方否认：接收方否认接受过消息

消息验证的主要目的是验证收到的消息确实来自真正的发送方并且未被修改，认证的过程通过认证符进行，产生认证符的函数称为认证函数，认证函数可以分为三类：

  • 消息加密：直接加密整个消息
  • 消息认证码MAC：通过MAC函数处理消息，将结果作为认证符
  • HASH函数：将hash函数当成认证符

主要使用的是Hash

消息加密

对称加密

例如对每个消息附加一个错误检测码，或称之为帧校验序列FCS

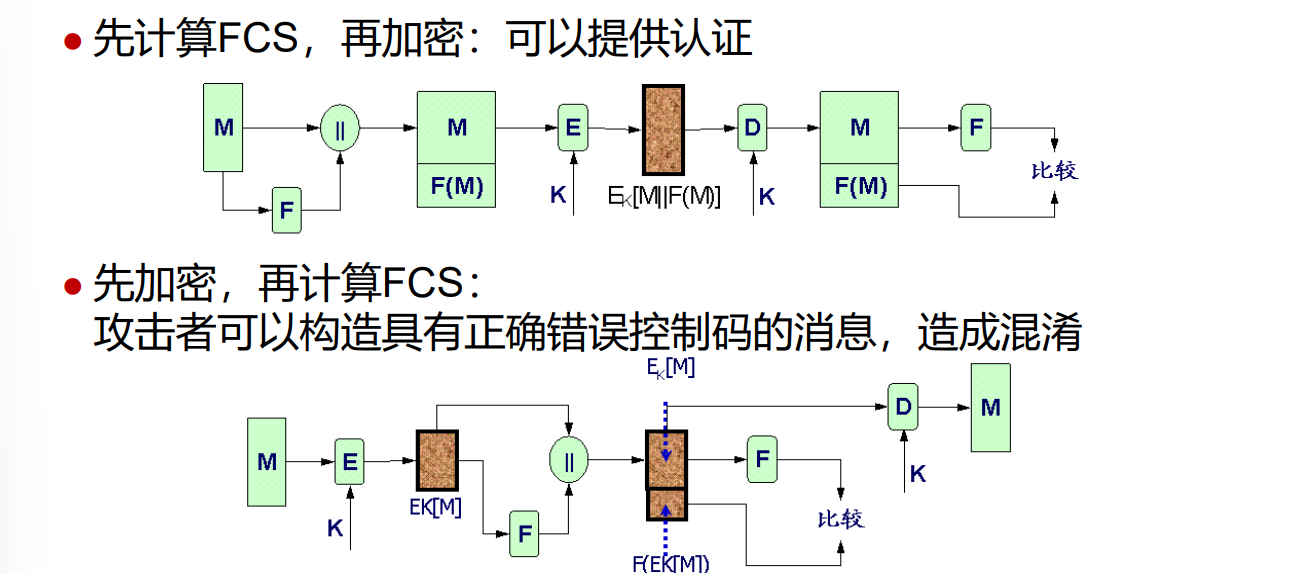
利用FCS进行对称加密
利用FCS进行对称加密

实际应用：TCP/IP协议

公钥加密

可以提供保密性，如果需要提供认证（数字签名），则发送方需要首先利用自身的私钥进行加密，再利用接收方的公钥进行加密

消息验证码MAC

MAC类似于一个加密函数，但是不要求可逆性，它利用密码生成一个固定长度的短数据块，并将该数据块附加在消息之后

发送方与接收方共享一个密钥K，发送方将消息的MAC附在消息之后，接收方也对消息计算MAC，判断是否被修改

当然我们也可以将携带了MAC的消息进行加密，或者将加密后的消息计算MAC，来达到认证+保密的效果

  • 将同一消息广播给很多接受者
  • 在信息交换中，接受者随机对消息进行认证
  • 对明文形式的计算机程序进行认证
  • 只需要认证而不需要保密：如SNMPv3
  • 需要将认证和保密性分开处理

肉丁土豆

hash码也称为消息摘要(Message Digest, MD)

用于认证的方法

  • 将消息hash之后连接，再用对称密码加密，对称密码用于认证，hash用于保密
  • 将消息hash之后用对称密码加密，再附在消息后，本质上就是一种MAC
  • 将消息hash之后用发送方的私钥加密，再附在消息后，提供了数字签名与认证能力
  • 将消息hash之后用发送方的私钥加密，附在消息后，再使用对称密码加密，提供了签名、认证与保密性
  • 发送方与接收方共享秘密值SS，将SS附在消息后再hash，而不直接通信SS
  • 发送方与接收方共享秘密值SS，将SS附在消息后再hash，得到的结果用对称密码加密

hash特点

H:M→HH: \mathcal{M} \to \mathcal{H}是满足如下条件的映射：

  • M=Σ∗\mathcal{M} = \Sigma^{*}
  • H={w ∣ len(w)≡n(const)}\mathcal{H} = \{w\,|\,\mathrm{len}(w) \equiv n\rm(const)\}
  • ∀m∈MH(m)\forall m \in \mathcal{M}\quad H(m)是可计算的
  • ∀h∈HH−1(h)\forall h \in \mathcal{H}\quad H^{-1}(h)是不可计算的
  • 给定mm，找到m′≠mm'\neq m使得H(m)=H(m′)H(m) = H(m')是不可计算的，称为抗弱碰撞
  • 找到任何x≠yx\neq y使得H(x)=H(y)H(x) = H(y)是不可计算的，称为抗强碰撞

一般结构

一般迭代地进行计算，给定一个初始值CV0\mathrm{CV}_{0}，将输入分为等长的LL组，最后一组如果长度不足则padding：

H(m)=CVLCVi=f(CVi−1,Yi−1)\begin{align*} H(m) &= \mathrm{CV}_{L} \\ \mathrm{CV}_{i} &= f(\mathrm{CV}_{i-1}, Y_{i-1}) \end{align*}

ff称之为压缩函数，本质上我们需要找到合适的ff

MD5

一种针对32位，倾向于小端机的算法

  • 输入：任意长度
  • 分组长度：512比特
  • 输出长度：128比特
  1. 增加填充位
    直接在整个消息之后填充10∗10^{*}，使得填充后消息的长度ll满足：

    l≡448 mod 512l \equiv 448 \text{ mod } 512

  2. 填充长度
    设第一步之后的报文长度为ll，则用64位二进制数表示l mod 264l\text{ mod } 2^{64}，并将结果附在最后，得到总长度是512倍数的消息
  3. 初始化缓存
    初始化用于存储CV\mathrm{CV}的128位缓冲区，使用4个32位寄存器表示，初始值为：
    • 32'h01234567
    • 32'h89abcdef
    • 32'hfedcba98
    • 32'h76543210
  4. 迭代计算
    MD5迭代过程
    MD5迭代过程
    每次迭代即为：

    c,d,a←b,c,db←a+((a+gcd(b,c,d)+XK+Ti)<<<3)\begin{align*} c, d, a &\leftarrow b, c, d \\ b &\leftarrow a + ((a + gcd(b, c, d) + X_{K} + T_{i}) <<< 3) \end{align*}

    逻辑函数为：
    • F(b,c,d)=(b⊕c)∨(¬b⊕d)F(b, c, d) = (b\oplus c)\vee(\neg b \oplus d)
    • G(b,c,d)=(b⊕d)∨(c⊕¬d)G(b, c, d) = (b\oplus d)\vee(c \oplus \neg d)
    • H(b,c,d)=b⊕c⊕dH(b, c, d) = b\oplus c\oplus d
    • I(b,c,d)=c⊕(b∨¬d)I(b, c, d) = c\oplus (b\vee \neg d)
  5. 输出

SHA

SHA即Secure Hash Algorithm，其基于MD4算法，因此大部分环节和MD算法是类似的

SHA-1输入少于2642^{64}位，输出为160位，分组长度512位

  1. 增加填充位
  2. 填充长度
  3. 初始化MD缓存
  4. 迭代计算，十轮压缩分为两组，每轮执行16迭代20步
  5. 输出
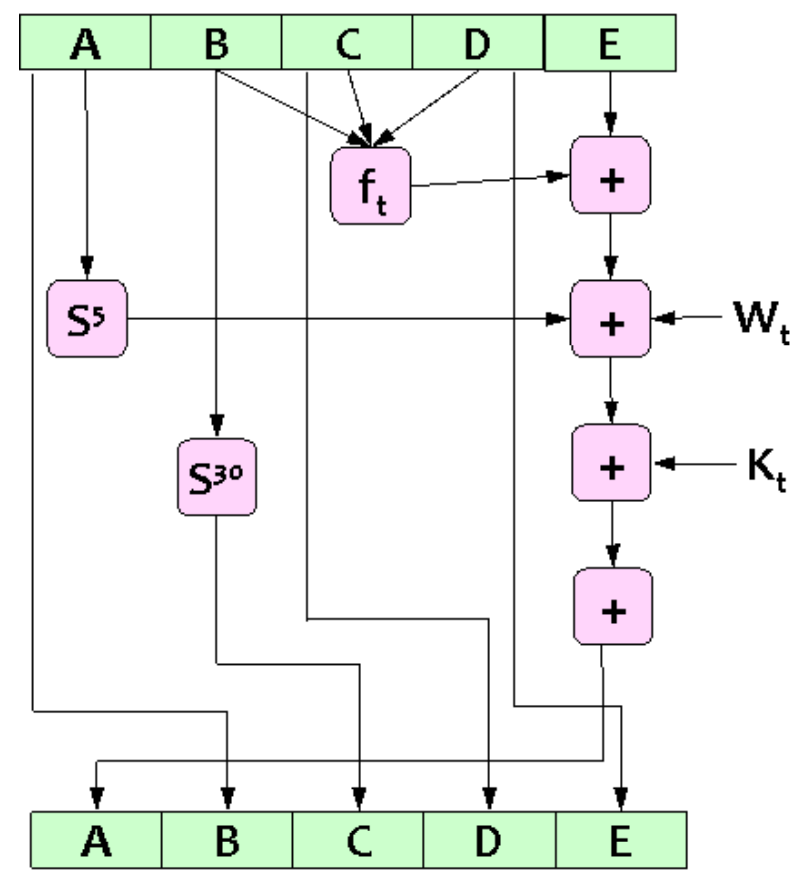
SHA压缩函数
SHA压缩函数

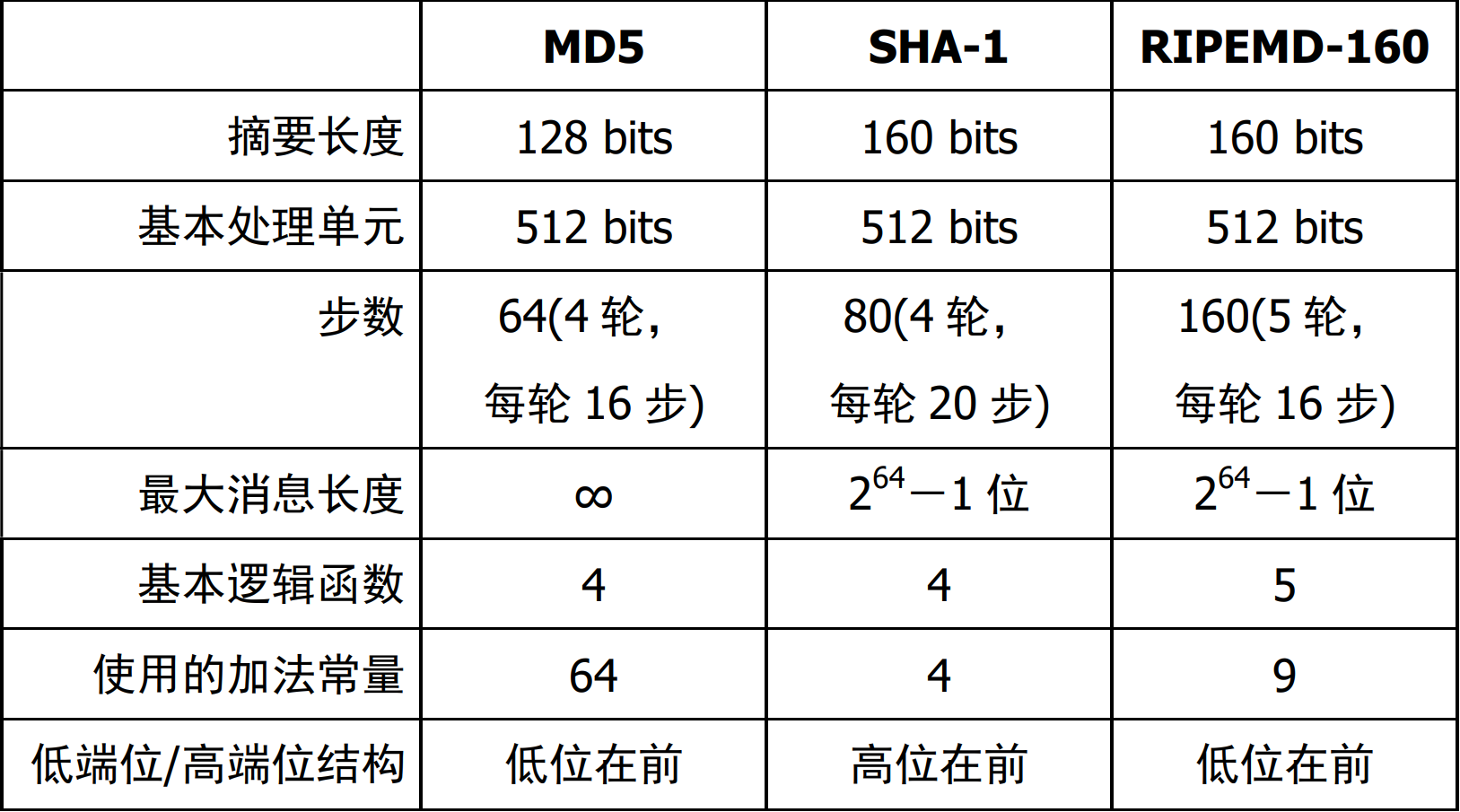
RIPEMD-160

RIPEMD-160输入任意长（这里和后面的表冲突了），输出为160位，分组长度512位

  1. 增加填充位
  2. 填充长度
  3. 初始化MD缓存
  4. 迭代计算，每轮16步迭代
  5. 输出
Hash函数比较
Hash函数比较

数字签名算法DSS

消息认证可以保证通信双方不收第三方的攻击，但是不能处理通信双方伪造消息或否认发送过消息，这个操作需要使用数字签名来完成，数字签名可以分为直接数字签名和仲裁数字签名

  • 直接数字签名：在加密之前首先利用发送方的私钥对数据或hash进行签名，这样解密后的数据就可以通过发送方的公钥验证签名
  • 仲裁数字签名：发送方将签名之后的消息发送给仲裁者，仲裁者验证签名之后，将消息加上日期与通过验证的标志，再发送给接收方

经典的数字签名标准DSS使用SHA-1算法

DSS算法
DSS算法

其中各个参数的含义为：

  • (p,q,g)(p, q, g)为全局公钥：
    • pp是LL位素数，LL满足512≤L≤1024512 \leq L \leq 1024且64 ∣ L64 \,|\, L
    • qq是160位的素数，并且是p−1p-1的因子
    • g=(h(p−1)/q) mod pg = (h^{(p-1)/q})\text{ mod }p，其中hh满足1<h<p−11 < h < p - 1，且hh需要使得g>1g > 1
  • 用户私钥xx：(0,q−1)(0, q - 1)之间的随机整数
  • 用户公钥yy：y=gx mod py = g^{x}\text{ mod }p
  • 签名私钥kk：(0,q)(0, q)之间的随机整数，每次签名随机一次
许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。