计算机网络安全技术 笔记 1

密码学基础

基本概念

传统加密 = 对称加密 = 单钥加密
安全性的来源是算法本身的保密性

现代加密 = 非对称加密 = 公钥加密
分离了算法与密钥

密码编码学的特征：

  1. 加密运算的运算类型：
    • 置换：打乱输入数据的顺序
    • 代换：将输入数据进行映射
  2. 所用的密钥数，即发送方与接收方使用的密钥是否相同
  3. 处理明文的方法：
    • 块密码 / 分组密码：按组处理数据
    • 流密码 / 序列密码：按比特处理数据

古典密码

代换密码

Caeser密码

对每个字母使用其后方的第3个字母代换

单表代换密码

单表代换代码：只有一张代换表，如Caeser与密钥词代码：设置一个密钥词放在前面，其余按照字母顺序

密钥词代码
密钥词代码

Playfair密码

多表代换密码，同样有一个密钥词，按照行优先的方式填充在一个5×55\times 5的矩阵内，剩余部分按顺序填充，i与j当成一个字母

加密方法：

  1. 每次加密两个字母，如果两个字母相同则更换后者为填充字，如果只剩一个字母同样填充，如：

balloon -> ba lx lo on

  1. 字母对落在同一行时，分别循环右移一位
  2. 字母对落在同一列时，分别循环下移一位
  3. 反之，对换两个字母的列

Hill密码

将字母指定为特定的数字，之后对原文序列做线性变换，因此密钥即为变换矩阵KK

优势为完全隐藏了单字母的频率特性，并且矩阵越大，隐藏的信息就越多，例如3×33\times 3矩阵隐藏了双字母的频率特性

Vigenere密码

多表代换密码的一种

Vigenere密码表
Vigenere密码表

对于密钥中的每一个字母，在上表中取出其所对应的加密表，之后循环使用密钥中的加密表来为明文进行加密

Vernam密码和一次一密

利用与明文相同长度的密钥进行加密，基于二进制数据而非字节：

ci=pi⊕kic_{i} = p_{i} \oplus k_{i}

当kk完全随机产生的时候，即为一次一密OTP，在理论上是牢不可破的，但是其在实际生活中几乎不可能实现

置换密码

常规的置换方法是按照密钥长度生成一个矩阵，并且按照行优先写入、列优先读出的规则，密钥决定了读出列的顺序

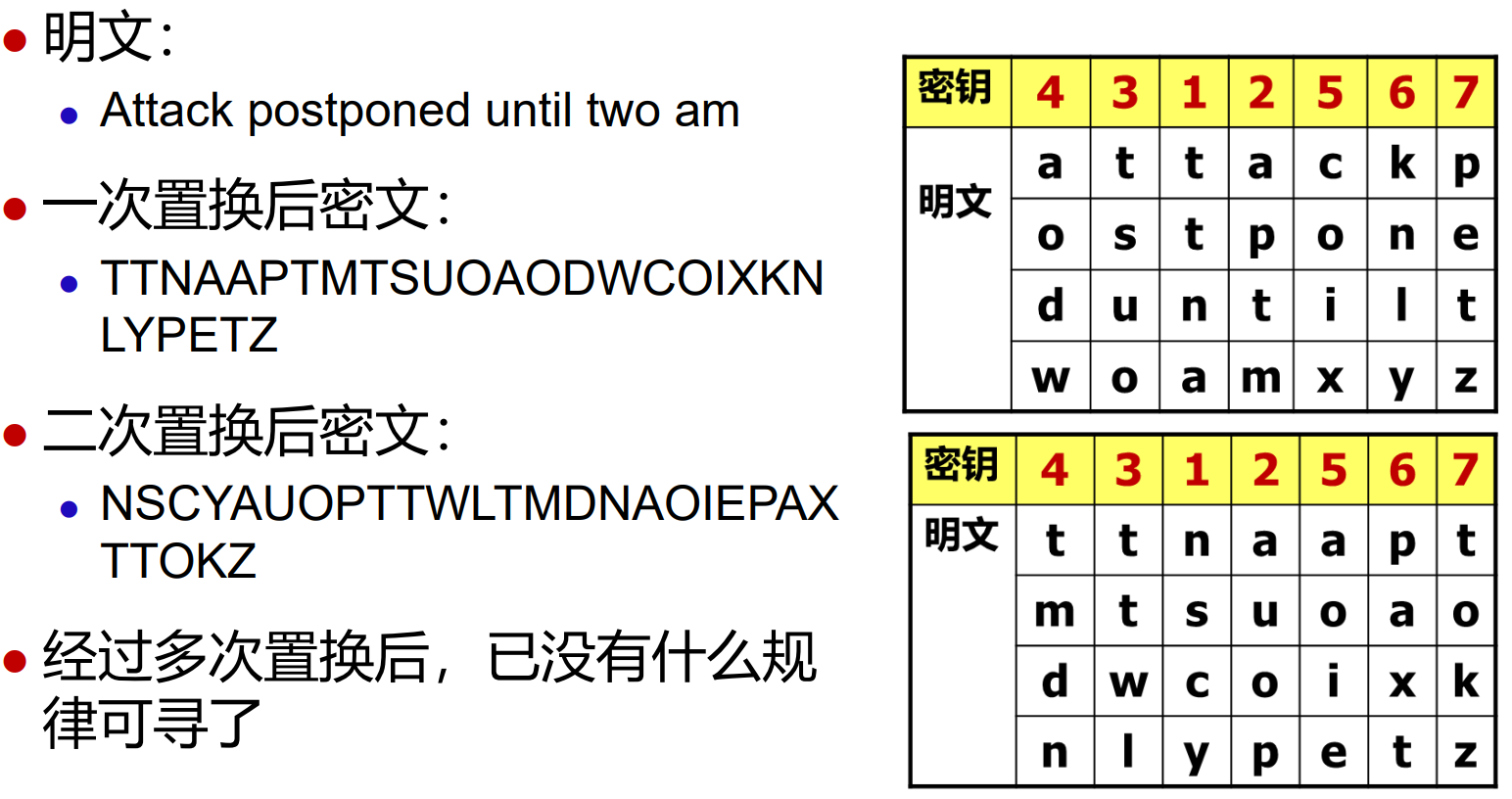
置换密码举例
置换密码举例

ENIGMA

Enigma结构示意图
Enigma结构示意图

三个滚轮对应三次单表代换，反射器负责使得编码和译码的过程完全对称，其并未增加复杂度

每次按下一个明文字母的时候，首先滚轮会转动（可能是左右移位），然后开始按照上面的路径依次读取，最后将结果显示在输出设备上

Enigma滚轮与反射器
Enigma滚轮与反射器

破译

基本方法有：

  • 穷举法：暴力，但是不能用于OTP
  • 频率分析法：利用字符的统计特性，例如在英语中最常出现的字母是e，q后方总是跟着u

对称密码

加密与解密使用同样的密钥，因此密钥需要使用私密信道进行分配

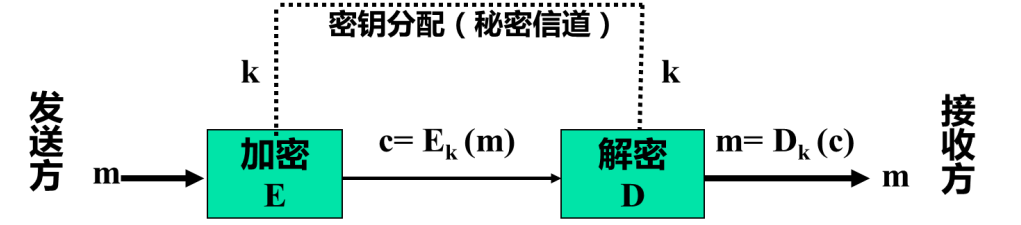
对称密钥算法
对称密钥算法

常见的对称密钥算法简介：

  • DES: Data Encryption Standard
  • IDEA: International Data Encryption Algorithm
  • RC 2/4/5
  • CAST-128
  • Blowfish

简化DES

加密算法：输入为一个8位明文组和10位密钥，输出8位密文组
解密算法：输出为一个8位密文组和10位密钥，输出8位明文组

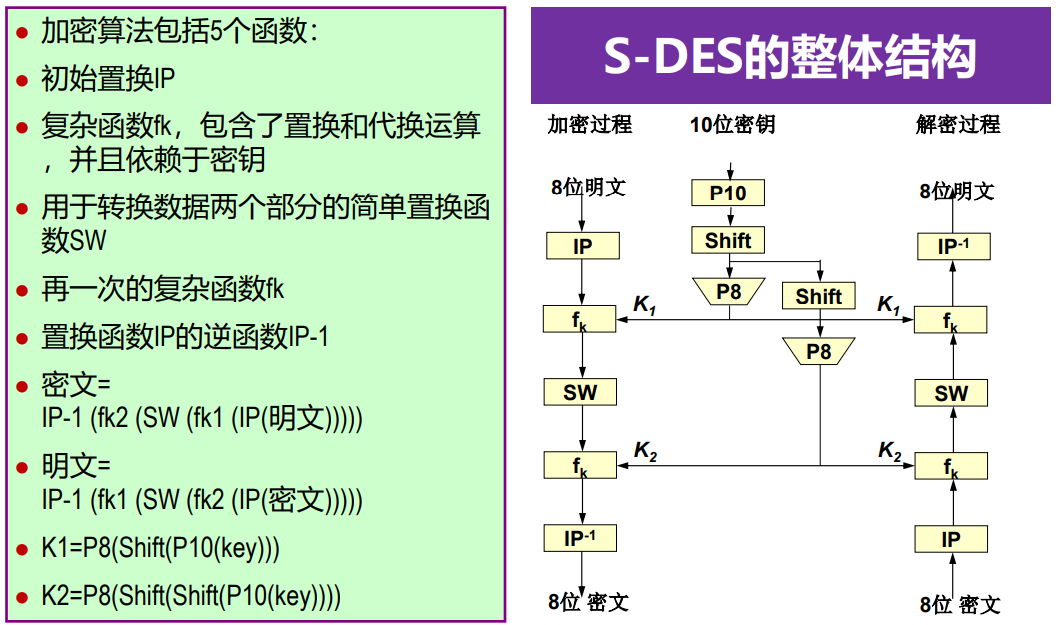
S-DES算法的整体结构
S-DES算法的整体结构

密钥的生成

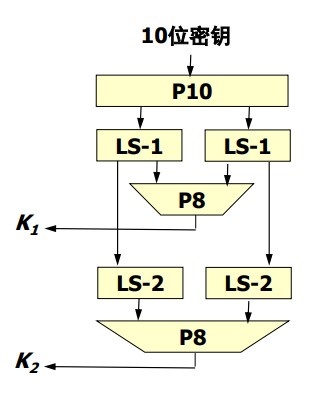
S-DES算法的整体结构
S-DES算法的整体结构
  1. P10置换定义为[1..10] -> [3, 5, 2, 7, 4, 10, 1, 9, 8, 6]
  2. LS-k指前5位与后5位分别循环左移k位
  3. P8定义为[1..10] -> [6, 3, 7, 4, 8, 5, 10, 9]

加密过程

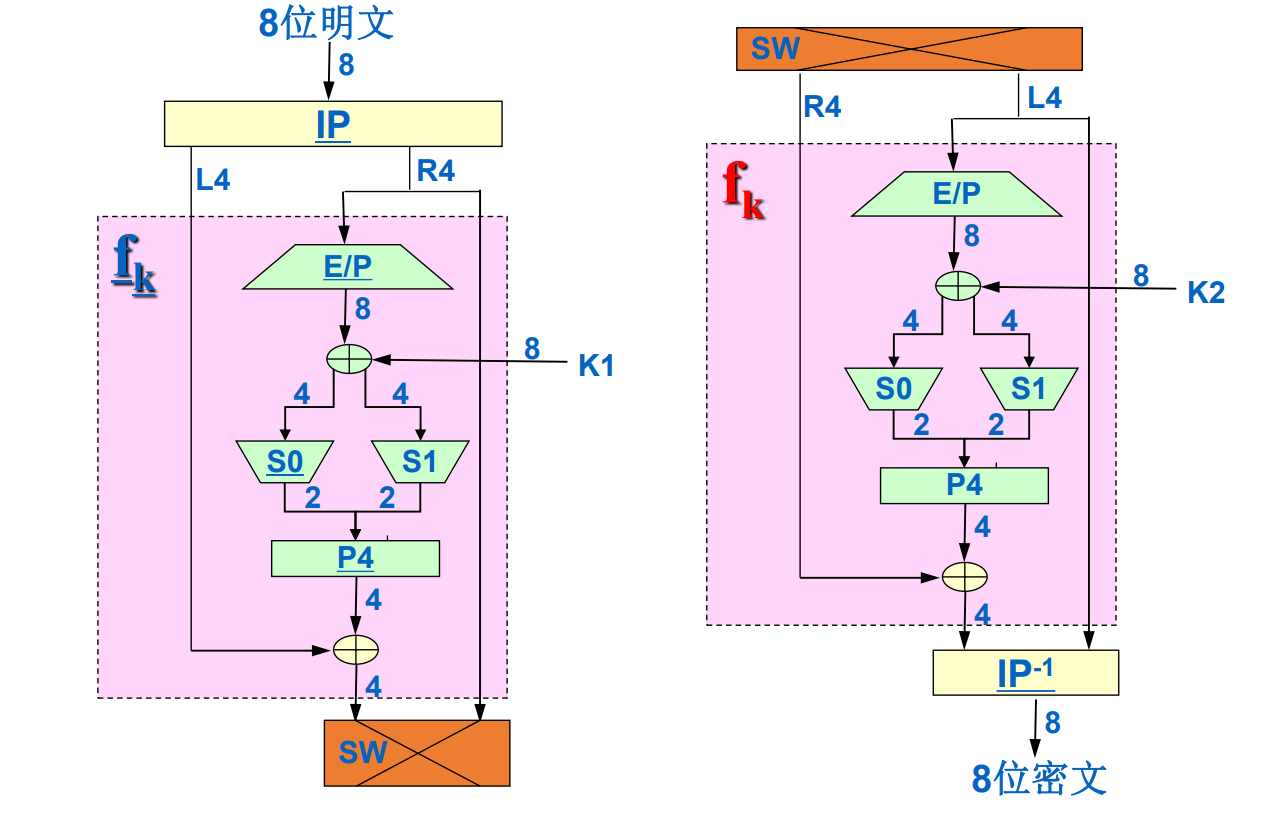
S-DES算法加密过程
S-DES算法加密过程
  1. 初始置换IP(1…8) = (2, 6, 3, 1, 4, 8, 5, 7)
  2. 扩展置换E/P(1…4) = (4, 1, 2, 3, 2, 3, 4, 1)
  3. ⊕\oplus代表异或操作
  4. Lk/Rk分别代表左k位与右k为
  5. S盒操作4输入2输出，S盒为4×44\times 4矩阵，输出为
    1
    2
    3
    row = 2 * input[0] + input[3]
    col = 2 * input[1] + input[2]
    output = '{0:b}'.format(S[row][col])
  6. S盒输出置换P4(1…4) = (2, 4, 3, 1)
  7. SW为交换左右4位
  8. 末尾置换IP−1^{-1}(1…8) = (4, 1, 3, 5, 7, 2, 8, 6)

Feistel密码

  • 建议使用乘积密码，即依次使用两个或以上的基本密码
  • 交替使用代换和置换

Shannon引入了混淆和扩散来刻画密码系统

  • 扩散是指将明文的统计信息消散在密文中
  • 混淆是指尽量使密文与密钥之间的关系更复杂

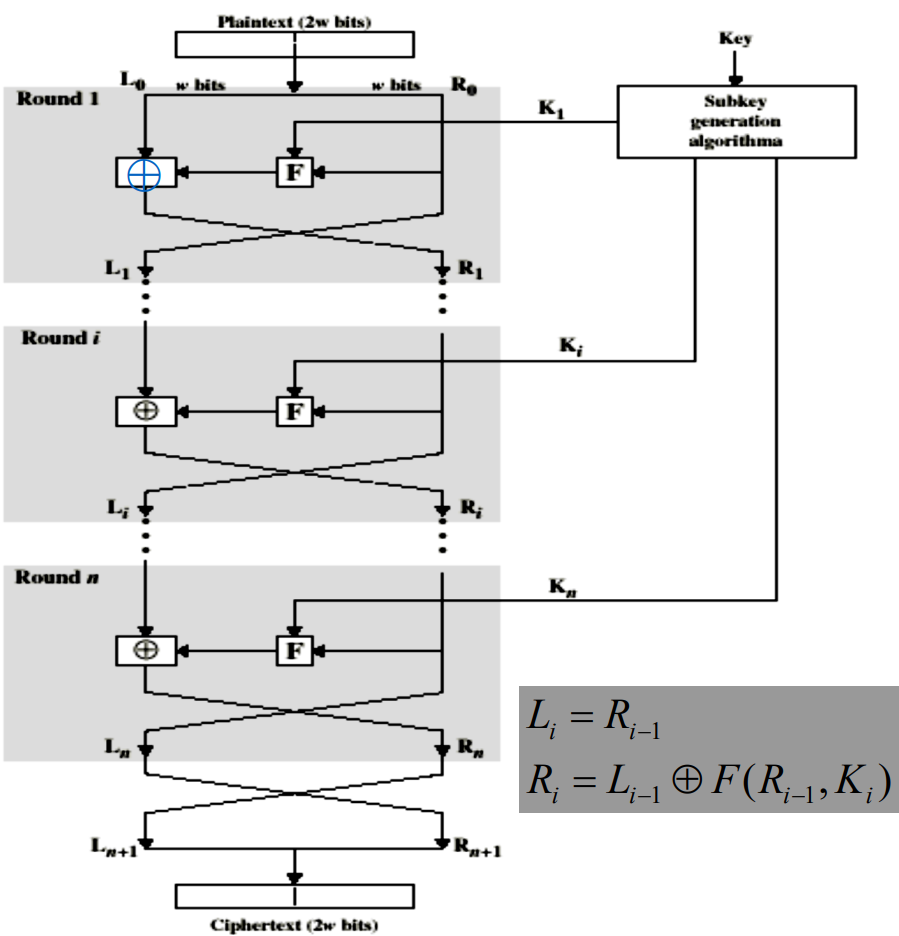
Feistel密码结构为：

  • 明文组等分成两部分，经过nn轮迭代合成密文组
  • 第ii轮输入为前一轮的输出
  • 子密钥由密钥经过相应算法推导出
Feistel密码结构
Feistel密码结构

DES密码

将明文分成64bits大小的块mm，执行如下操作

DES(m)=IP−1⋅T16⋯T1⋅IP(m)\mathrm{DES}(m) = \mathrm{IP}^{-1}\cdot T_{16} \cdots T_{1}\cdot \mathrm{IP}(m)

密钥的生成步骤为：

  • 拆分为两部分
  • 左移一定位数
  • 进行压缩置换 56bits→48bits\quad56\text{bits}\to 48 \text{bits}

每一轮的迭代步骤（即F函数）为：

  • E盒扩展置换32bits→48bits\quad32\text{bits}\to 48\text{bits}
  • 与对应轮次密钥异或
  • S盒代换选择，使用8个6进4出的S盒组成48bits→32bits\quad48\text{bits}\to 32\text{bits}
  • P盒置换
  • 与另一半输入异或

三重DES加密

密钥长度为112比特，即两个常规DES算法的密钥拼接得到

加密算法为：

C=Enc(k1,Dec(k2,Enc(k1,p)))C = \mathrm{Enc}(k_{1}, \mathrm{Dec}(k_{2}, \mathrm{Enc}(k_{1}, p)))

Blowfish算法

分组长度64位，密钥长度在32~448位之间

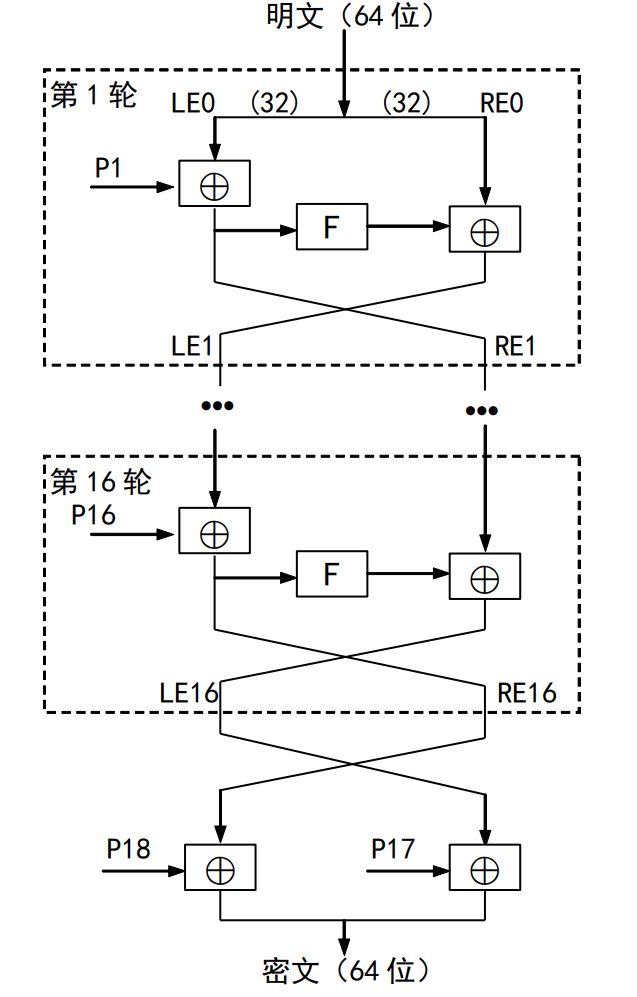
Blowfish加密过程
Blowfish加密过程

F函数包含了4个S盒运算，子密钥与S盒都是由算法本身生成的，并且对数据左右同时执行运算，复杂性更强

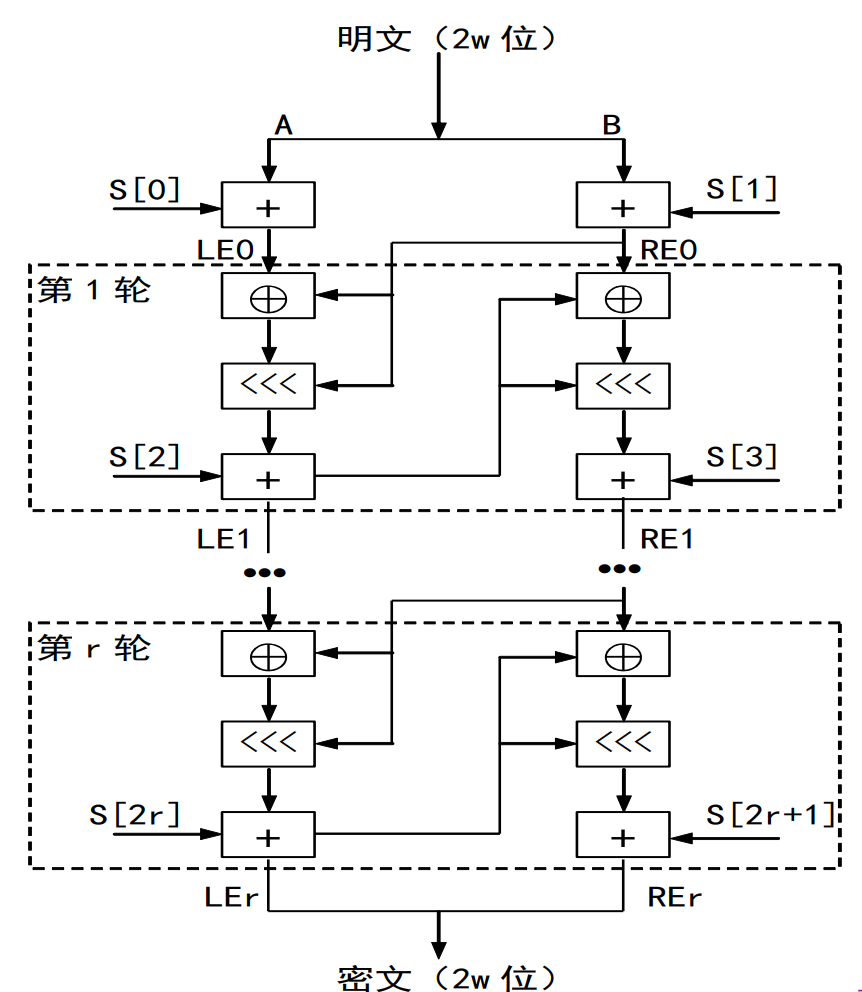
RC5

分组长度为32/64/128位，密钥长度0~2040位，参数有：

  • ww：分组长度
  • rr：迭代次数
  • bb：密钥的字节数
RC5加密过程
RC5加密过程

非对称密码

公钥密码体制：

  • 明文
  • 加密算法
  • 公钥 / 私钥
  • 密文
  • 解密算法

利用Alice的公钥加密的密文只能被Alice的私钥解密，因此只要Alice保证了私钥的私有性，即可保证密码的安全，公钥是公开的

同样的，Alice可以用自己的私钥对数据进行签名，这样其他人可以利用Alice的公钥解签名，验证其专有性

这两种方法也可以同时使用，如下图

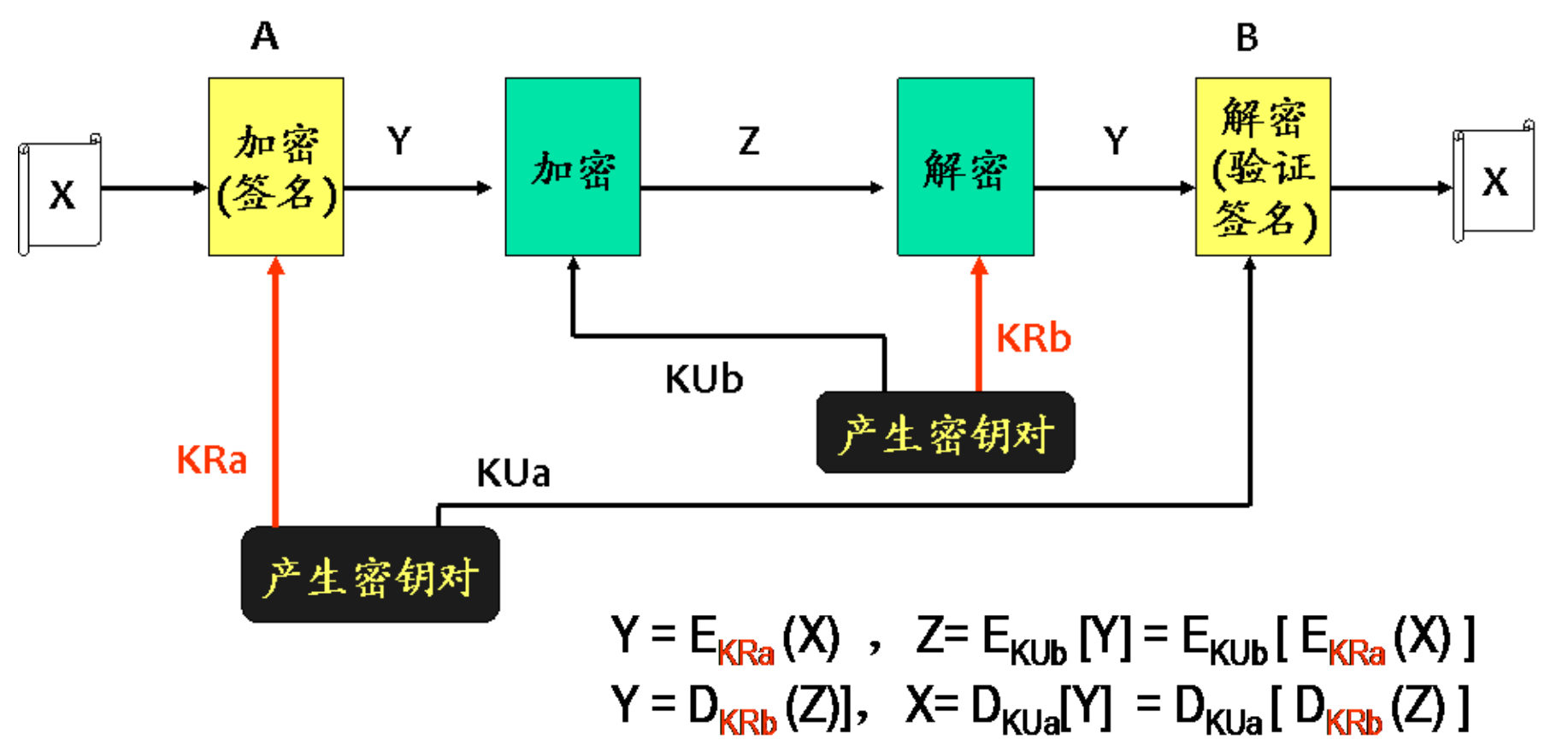
同时做签名与加密
同时做签名与加密

数学原理

公钥密码基于陷门单向函数，其是指满足下列条件的函数ff：

  1. y=f(x)y = f(x)是可计算的
  2. x=f−1(y)x = f^{-1}(y)是不可计算的
  3. ∃δ\exists\delta，当δ\delta已知的时候，x=f−1(y)x = f^{-1}(y)是可计算的

数论基础

欧拉函数φ(n)=∑i=1n1gcd(m,n)=1\varphi(n) = \sum\limits_{i=1}^{n}\mathbf{1}_{\mathrm{gcd}(m, n) = 1}

欧拉定理：

gcd(m,n)=1⇔mφ(n)≡1 mod n\mathrm{gcd}(m, n) = 1 \Leftrightarrow m^{\varphi(n)} \equiv 1 \text{ mod }n

推论：给定素数p≠qp\neq q，整数0<m<n=pq0 < m < n = pq，则∀k∈Z\forall k \in \mathbb{Z}

mkφ(n)+1≡m mod nm^{k\varphi(n) + 1} \equiv m \text{ mod }n

RSA算法

密钥的产生：

  • 取大素数p,qp, q，计算n=pqn = pq，公开nn
  • 计算φ(n)=(p−1)(q−1)\varphi(n) = (p-1)(q-1)
  • 取ee满足：gcd(e,φ(n))=1\mathrm{gcd}(e, \varphi(n)) = 1且1<e<φ(n)1 < e < \varphi(n)
  • 计算d<φ(n)d < \varphi(n)使得de≡1 mod φ(n)de \equiv 1 \text{ mod }\varphi(n)
  • 公钥为(e,n)(e, n)，私钥为(d,n)(d, n)

加密过程：将待解密的内容分为k≤log⁡2nk\leq \log_{2}n组，则密文为：C=Me mod nC = M^{e}\text{ mod }n

相对应的解密过程为：M=Cd mod nM = C^{d}\text{ mod } n

大素数质因数分解的困难性保证了这个算法的安全性，因此密钥越大，安全性越高，但是性能会越低

DH密钥交换算法

我们定义本原根：
aa是素数pp的本原根当且仅当{a,a2,…,ap−1} mod p={1,…,p−1}\{a, a^{2},\dots,a^{p-1}\}\text{ mod }p = \{1, \dots, p-1\}

对于素数pp，设其一个本原根为aa，取整数b<pb<p，则我们可以找到唯一的指数ii，使得b≡ai mod pb\equiv a^{i}\text{ mod }p，则ii称为bb以aa为底模pp的离散对数，记为i=inda,p(b)i = \mathrm{ind}_{a, p}(b)

离散对数满足：计算bb是简单的，但是计算ii非常困难

DH算法可以且仅可以用于密钥交换

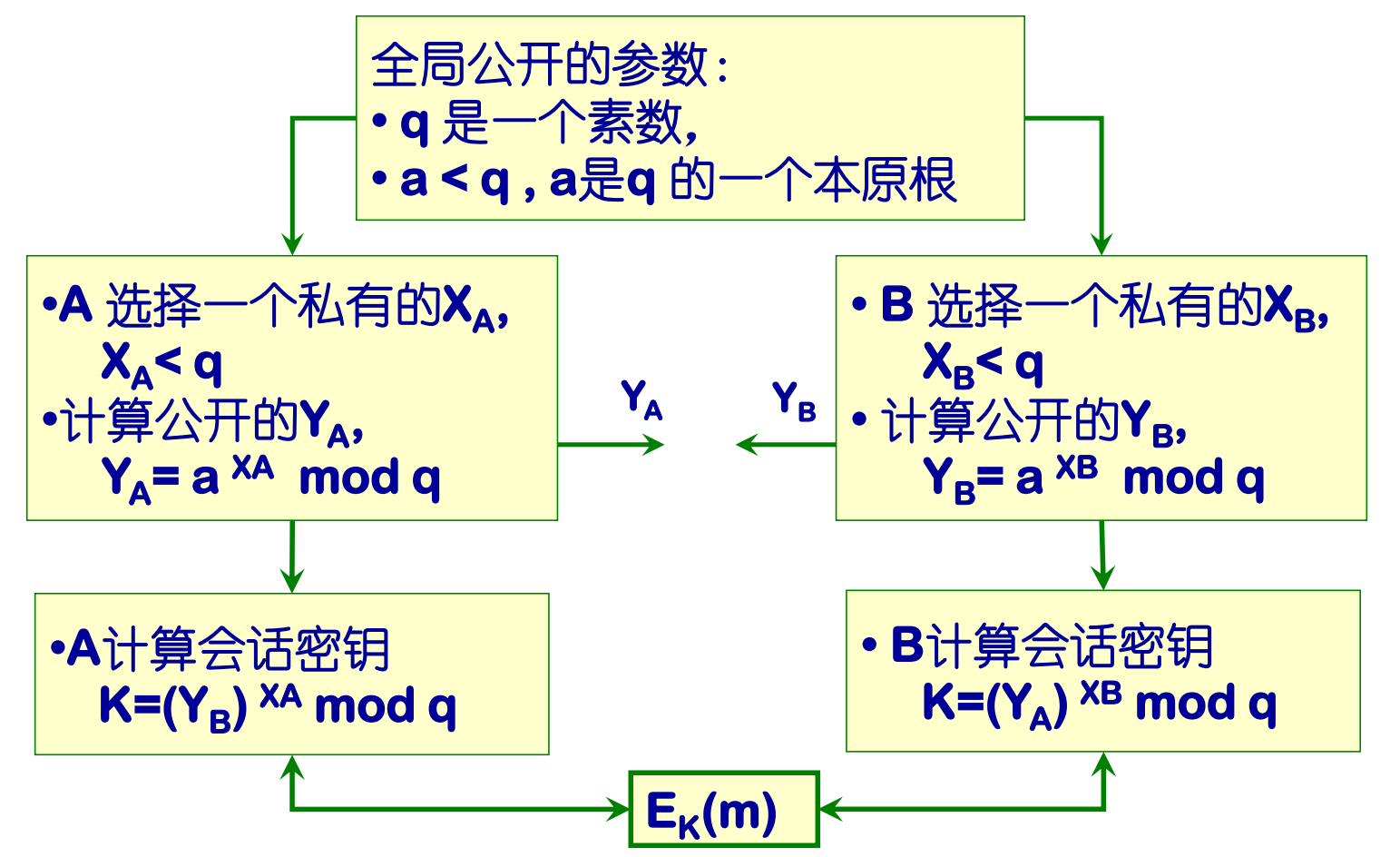
DH密钥交换算法
DH密钥交换算法

这样之后Alice与Bob同时知道了一个密钥KK，可以用于作为对称密码的密钥

密钥分配

传统的对称密码分配

最朴素的方法有人工传送密钥，但是这样只适用于链路加密，并且被破译的概率可能更大，如果对于端对端加密，则需要KDC

密钥分配中心KDC

假定每个用户与KDC共享唯一的一个主密钥，则Alice和Bob获得会话密钥KsK_{s}的过程是：

  1. Alice向KDC请求会话密钥以保护与Bob的逻辑连接，提供Alice与Bob的标识和临时交互号N1N_{1}
  2. KDC用KaK_{a}加密响应并告知Alice，其中包括Ks,N1,EncKb(Ks,IdA)K_{s}, N_{1}, \mathrm{Enc}_{K_{b}}(K_{s}, Id_{A})
  3. Alice解密，利用N1N_{1}分割信息，前一段为KsK_{s}，后一段转发给Bob
  4. Bob使用KbK_{b}解密即可

当网络规模过大的时候，使用层次式的KDC，类比ISP

公钥的分配

公开发布

即通信方直接公布自己的公钥，非常简便，但是容易被伪造

公开可访问目录

由管理员维护一个dict[name, public_key]，定期发布或者更新该目录

通信方通过管理员来注册公钥，可以随时更新自己的公-私钥对，并且可以通过与管理员的安全认证通道来访问公钥目录

这种方法的弱点在于目录管理员本身

公钥授权

由管理员来控制

  1. A发送带有时间戳的信息请求B的公钥
  2. 管理员发送用自己私钥加密的消息，包括B公钥、原始请求与原始时间戳
  3. A保存B公钥，将A的标识和临时交互号发给B（用于确认身份）
  4. B同样从管理员处获得A的公钥
  5. A B通过临时交互号确认身份，开始通信

这种方法的瓶颈在与每次都要向管理员申请公钥

公钥证书

证书包含公钥和一些其他信息，由证书管理员产生并发给对应通信方，这样该通信方可以通过传递证书将密钥信息传递给另一方

证书需要满足的条件是：

  • 任何通信方都可以读取证书并确定拥有者的姓名和公钥
  • 任何通信方都可以验证证书的真伪性
  • 任何通信方都可以验证证书的时效性
  • 只有管理员可以产生、更新证书

利用公钥分配传统密码的密钥

直接分配

最简单的一种方法，但是容易受到主动攻击

  • A向B发送自己的公钥和标识
  • B计算KsK_{s}，用A的公钥加密后发给A
  • A解密得到KsK_{s}

安全分配

  • A和B交换公钥
  • A用B的公钥对含有A标识和临时交互号N1N_{1}的消息加密，发给B
  • B用A的公钥对N1N_{1}和临时交互号N2N_{2}加密，发给A
  • A用B的公钥对N2N_{2}加密，发给B（这一步之后可以让双方确认身份）
  • A计算密钥KsK_{s}，依次用A私钥、B公钥加密后发给B
  • B解密得到KsK_{s}
许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。