人智导 神经网络与机器学习

神经网络

多层神经网络示意图
多层神经网络示意图

神经元

接收输入x⃗\vec{x}，计算net=w⃗⋅x⃗+bnet = \vec{w} \cdot \vec{x} + b，之后使用激活函数gg对其进行激活（限制其值域范围）

常见的激活函数有：

  • 符号函数sgn\mathrm{sgn}
  • Sigmoid函数σ(z)=11+e−z\sigma(z) = \frac{1}{1 + e^{-z}}
  • 双曲正切函数tanh⁡(z)=ez−e−zez+e−z\tanh(z) = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}}
  • 线性整流函数ReLU(z)=max⁡{0,z}\mathrm{ReLU}(z) = \max\{0, z\}

输出归一化

采用Softmax函数将输出层netinet_{i}归一化：

oi=eneti∑k=1menetko_{i} = \frac{e^{net_{i}}}{\sum\limits_{k=1}^{m}e^{net_{k}}}

全连接网络

隐含层之间是全连接的神经网络

训练方式为：

  1. 构建数据集，划分为训练集与验证集（实际应用的数据被称为为测试集，我们在训练阶段理应不能得到这批数据）
  2. 选择损失函数，通常选用误差平方和或交叉熵，误差平方和为：

    E(w⃗)=12∑d=1n∑k=1m(tkd−okd)2E(\vec{w}) = \frac{1}{2}\sum\limits_{d=1}^{n}\sum\limits_{k=1}^{m}(t_{kd} - o_{kd})^{2}

  3. 训练：求损失函数最小值，一种算法为梯度下降：

    wi⇐wi−η∂E∂wiw_{i} \Leftarrow w_{i} - \eta \frac{\partial E}{\partial w_{i}}

    也即：

    w⇐w−η(∇wE)w \Leftarrow w - \eta(\nabla_{w}E)

    梯度下降分为批量、小批量、随机样本三种，差距在与每次处理的样本个数

梯度的计算

随机梯度下降中最麻烦的问题在于梯度的计算，主要思想是链式法则与反向传播，以激活函数为σ\sigma为例，具体来说，算法为：

  1. 随机初始化为权重为较小随机值
  2. 给定样本，计算所有输出
  3. 对于输出层第jj个元素，有：

    ∂E∂wji=∂E∂oj∂oj∂netj∂netj∂wji=−(tj−oj)oj(1−oj)xji=−δjxji\begin{align*} \frac{\partial E}{\partial w_{ji}} &= \frac{\partial E}{\partial o_{j}} \frac{\partial o_{j}}{\partial net_{j}} \frac{\partial net_{j}}{\partial w_{ji}} \\ &= -(t_{j} - o_{j})o_{j}(1-o_{j})x_{ji} \\ &= - \delta_{j}x_{ji}\end{align*}

  4. 更新权重
  5. 对于隐含层第jj个元素，有：

    ∂E∂wji=∑k∈succ(j)(∂E∂netk∂netk∂oj∂oj∂netj)∂netj∂wji=−∑k∈succ(j)(δkwkjoj(1−oj))xji=−δjxji\begin{align*} \frac{\partial E}{\partial w_{ji}} &= \sum\limits_{k \in \text{succ}(j)}\biggl(\frac{\partial E}{\partial net_{k}} \frac{\partial net_{k}}{\partial o_{j}} \frac{\partial o_{j}}{\partial net_{j}}\biggr) \frac{\partial net_{j}}{\partial w_{ji}} \\ &= -\sum\limits_{k \in \text{succ}(j)}\bigl(\delta_{k}w_{kj}o_{j}(1-o_{j})\bigr)x_{ji} \\ &= -\delta_{j}x_{ji}\end{align*}

  6. 更新权重

交叉熵

交叉熵损失函数为：

H(w)=−∑d=1N∑k=1Mtkdlog⁡(okd)H(w) = -\sum\limits_{d=1}^{N}\sum\limits_{k=1}^{M}t_{kd}\log(o_{kd})

其中okdo_{kd}为实际值，要求是概率，因此其输入层需要经过一次softmax

平方和损失函数常用于输出是具体数值的问题，交叉熵损失函数用于分类问题

卷积神经网络

全连接的不足：参数过多，影响速度与效率

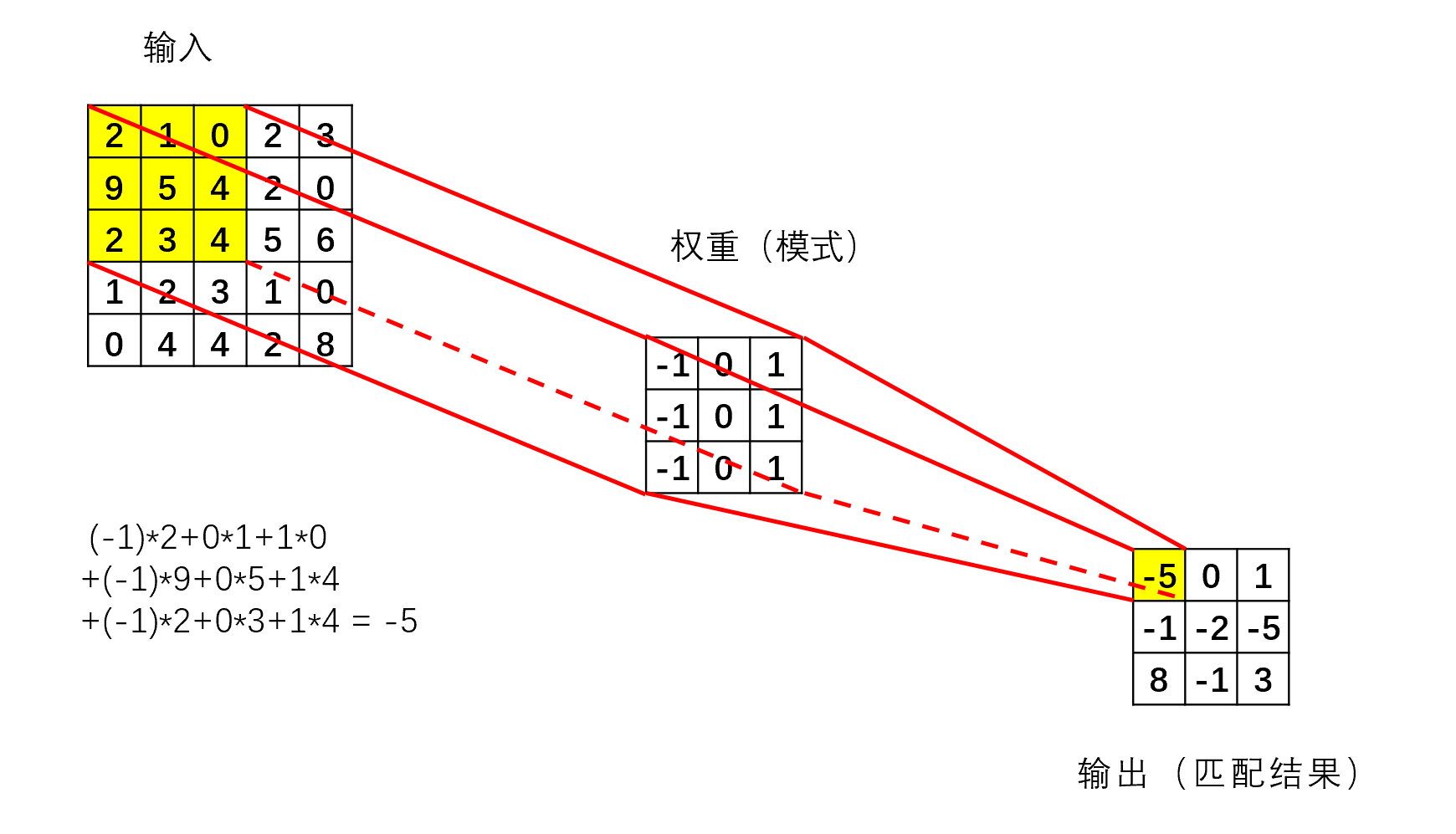
卷积示意图
卷积示意图

因此卷积神经网络利用卷积核对于输入数据进行卷积，降低输出维数，卷积核通过训练得到，并且卷积核是共享的，也即对于同一组数据的不同部分其参数值不变

填充与步长

填充为在原输入的最外围填充若干圈00来增加维数，例如5×55\times 5变为7×77 \times 7

步长为卷积核每次滑动的距离，必须要保证卷积核被完整的包含在输入当中

多卷积核与多通道

多个卷积共同卷同一个数据，每个卷积产生一个通道，通道数等于卷积核数

当输入为多通道时，例如6×6×36\times 6\times 3，卷积核的深度一定要与之一致，即x×y×3x \times y \times 3

池化

降维的手段，通常是将一定的区域压缩为一个值，通常包括最大池化、平均池化等，窗口的大小与步长都可以设置

最大池化示意图
最大池化示意图

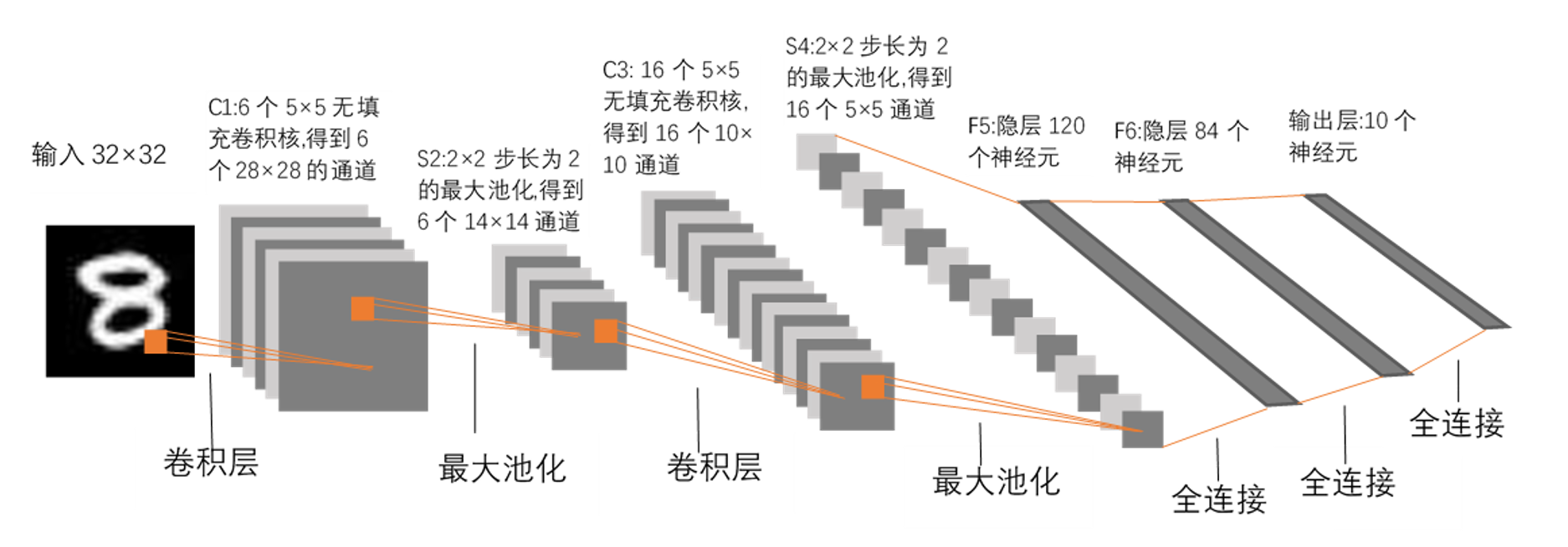
实例

两个实例

LeNet神经网络
LeNet神经网络
VGG-16神经网络
VGG-16神经网络

总结

卷积神经网络总结：

  • 卷积核能够提取特征
  • 参数较少

梯度消失问题

神经网络的主要问题之一

在BP中，我们有：

δh=oh(1−oh)∑k∈succ(h)δkwkh≤14∑k∈succ(h)δkwkh\delta_{h} = o_{h}(1 - o_{h})\sum\limits_{k\in \mathrm{succ}(h)}\delta_{k}w_{kh} \leq \frac{1}{4}\sum\limits_{k\in \mathrm{succ}(h)}\delta_{k}w_{kh}

因此层数过多的时候，梯度将以指数级下降，一种解决思路是采用ReLU\mathrm{ReLU}

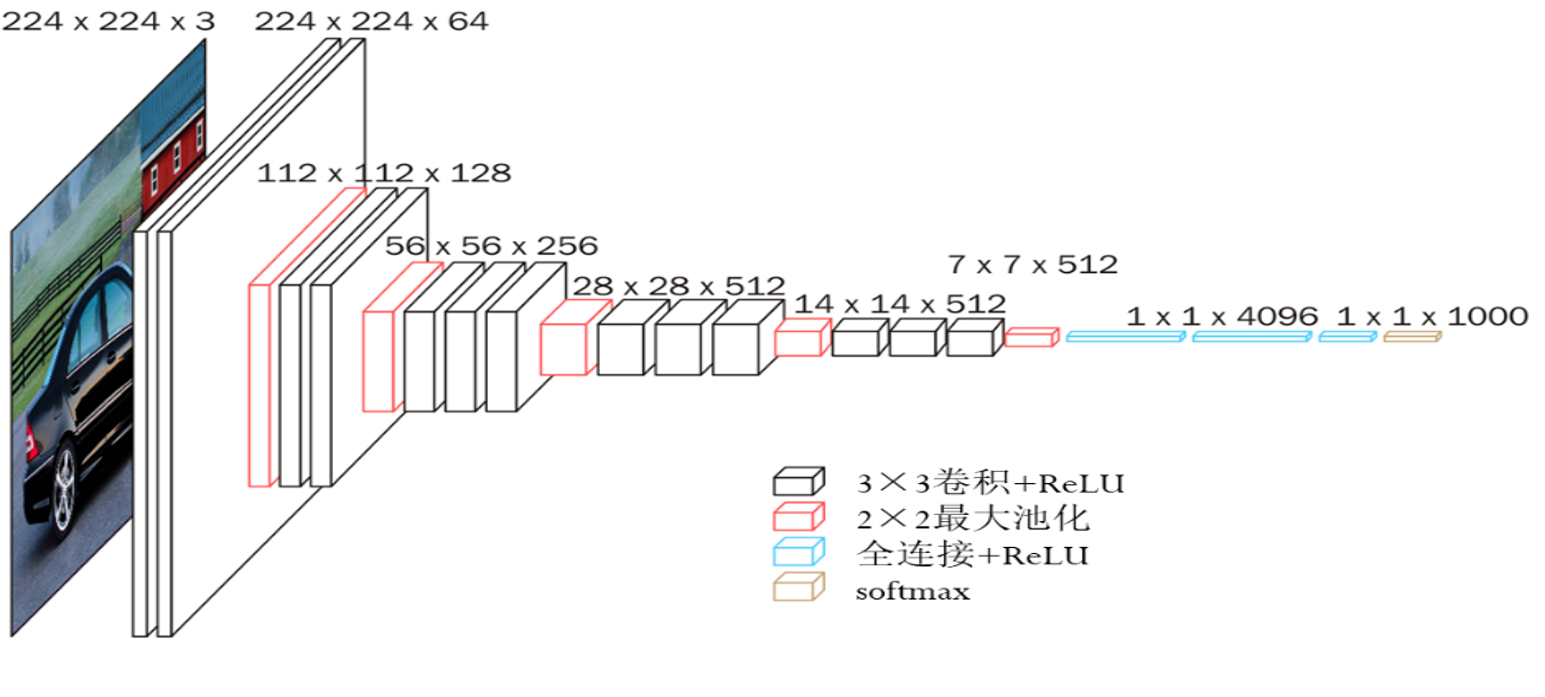
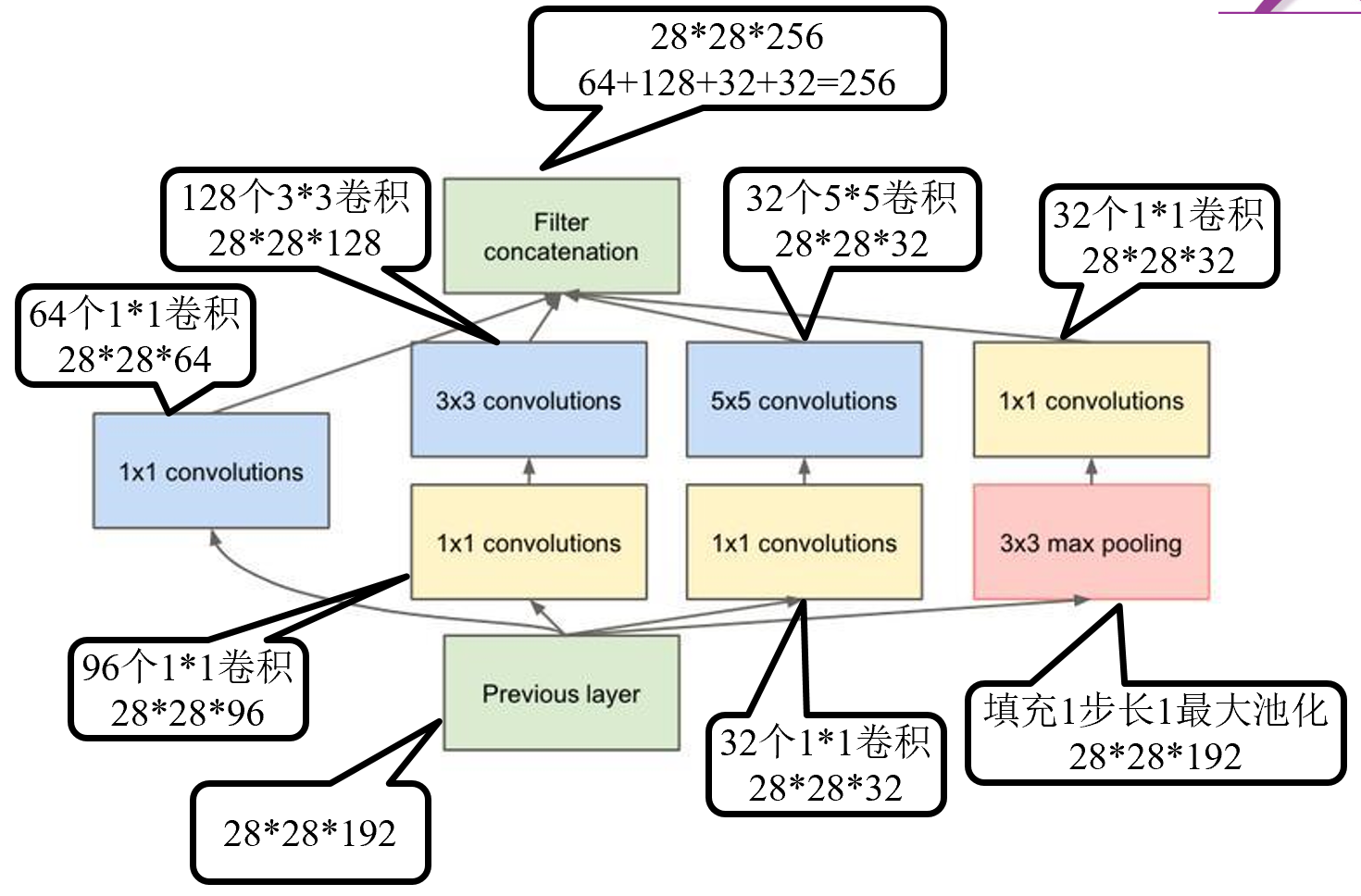
两个实例

GoogLeNet中的Inception模块
GoogLeNet中的Inception模块

利用1×11\times 1等卷积核改变通道数之后拼接起来，相当于在参数尽可能少的情况下减弱梯度消失的问题

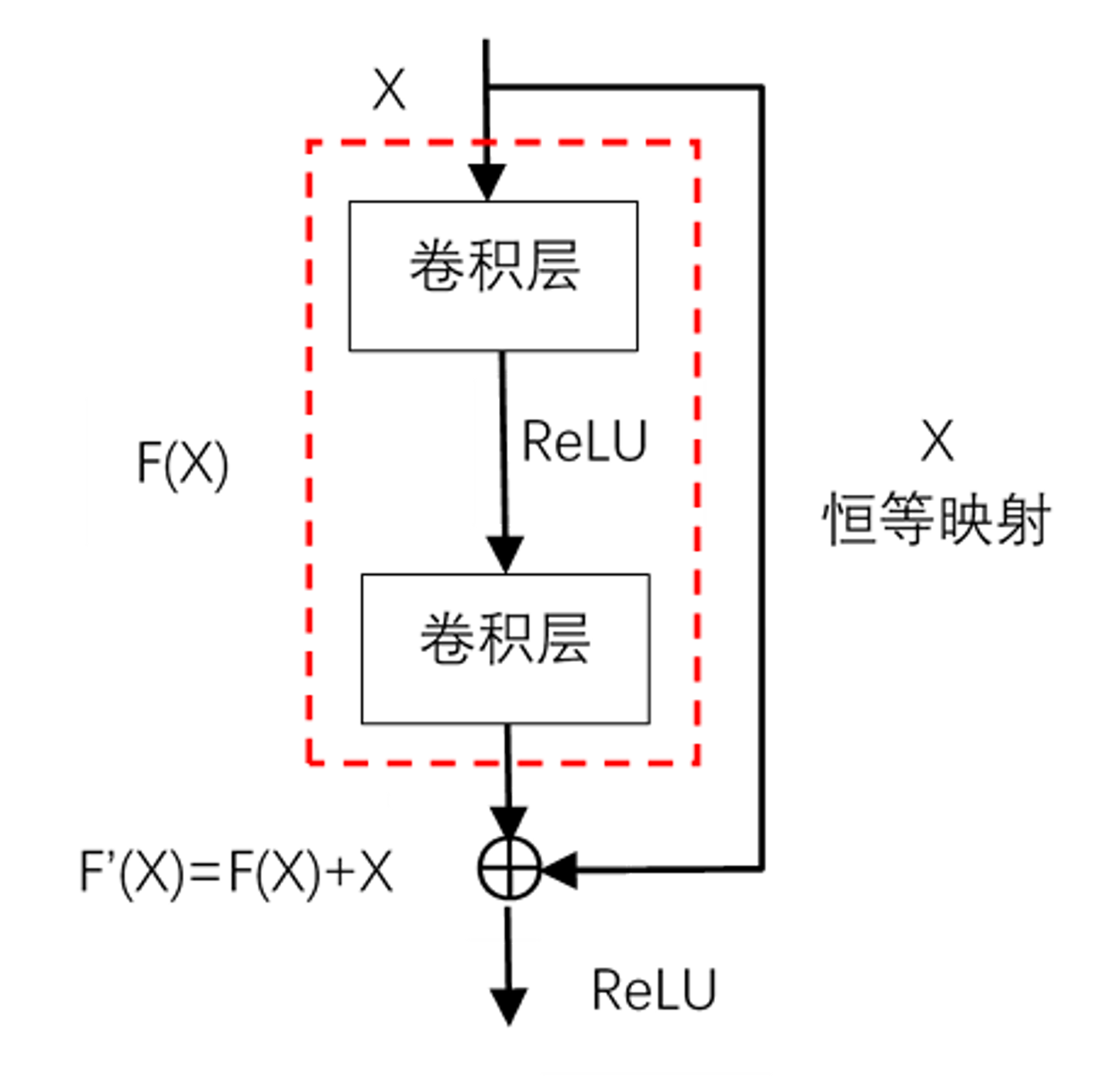
残差网络中的残差模块
残差网络中的残差模块

在残差网络中，在一层的常规计算结束之后，将计算结果与输入取加和得到下一层的输入，这样可以一定程度上避免神经网络发生退化（层数过多导致再增加层数的时候效果提升不显著）

注意要求F(X)F(X)与XX的维数、通道数必须相同，因此需要对二者进行相应的填充

过拟合问题

对于训练集数据过拟合，训练出的模型不具有普适性，解决方法有：

  • 使用验证集，个人理解是利用验证集来模拟测试集，在训练集上训练，在验证集上防止过拟合
  • 正则化项法：将损失函数加上正则化项∣∣w⃗∣∣2||\vec{w}||^{2}其中w⃗\vec{w}为所有的参数组成的向量，从而降低模型参数个数，降低模型复杂性
  • Dropout：随机临时舍弃一些神经元，使之不参与计算，减少参数量，舍弃率可调
  • 数据增强：增加数据量，将同一份数据进行多种变换，例如图像的缩放、旋转等等，也有非线性化等高级的做法

词向量

第一个问题：如何来表示词与文本

独热编码(One-hot)

用于词表等长的向量来表示词，第ii个词的第ii位为11，其余全00

优点：

  • 简单方便

缺点：

  • 编码太长
  • 无法度量相似性

分布式表示

稠密向量表示，向量的每一位代表一个特征，具体的数值代表这个词该种特征的强弱

克服了独热的两种问题，但是编码很困难，具体的值不容易找出，需要在训练过程中调整

语言模型

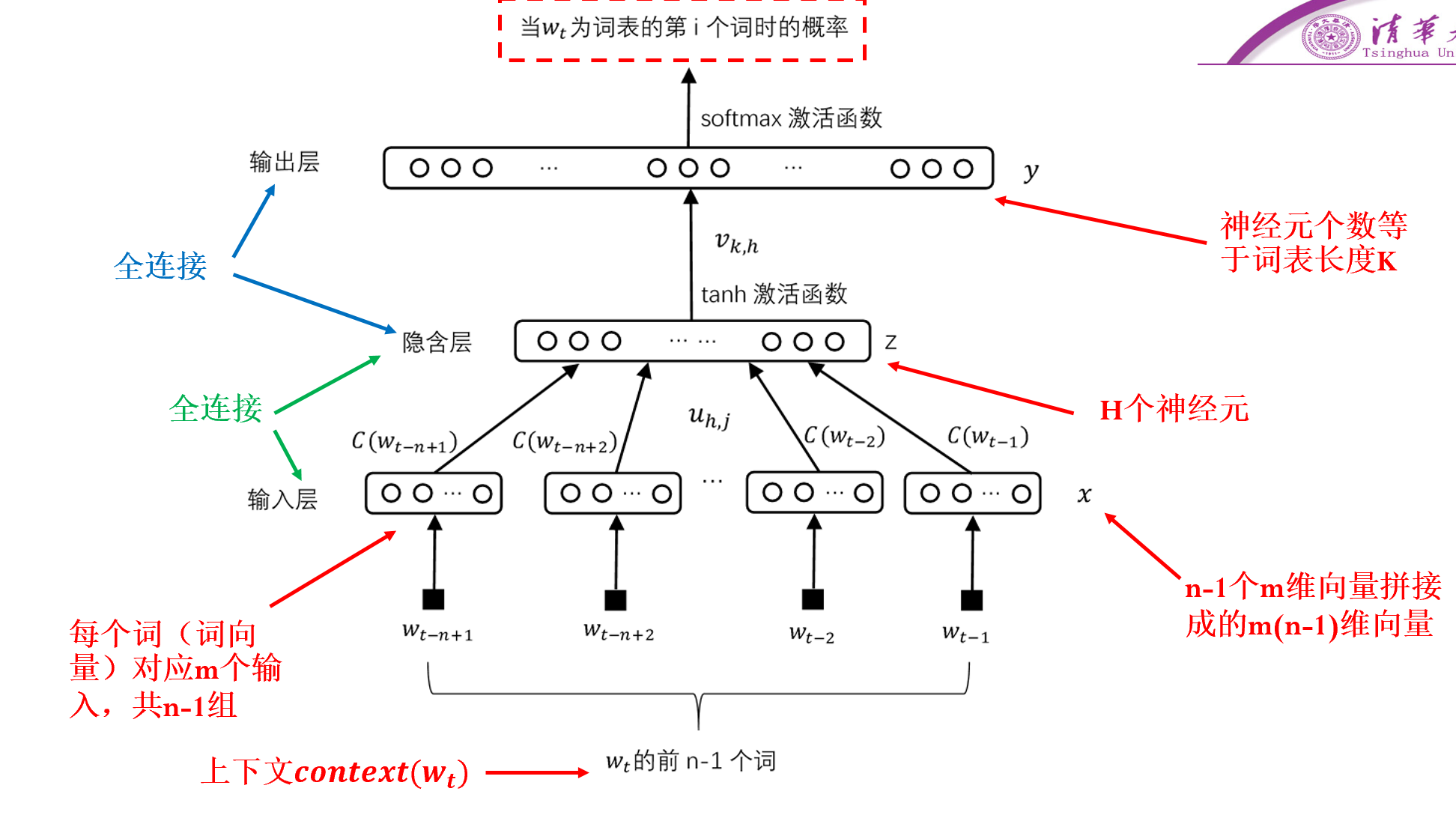
nn元语言模型是指，通过前n−1n - 1个词来推断下一个词，在神经网络中实现方式如下：

n元模型神经网络
n元模型神经网络

其中第一步为词嵌入得到词向量，具体的向量需要通过训练得到

参数的估计采用最大似然估计的方式，即：

max⁡θ∏w∈CP(w=k ∣ context(w),θ)\max\limits_{\theta}\prod\limits_{w\in C}P(w = k\,|\, \text{context}(w), \theta)

word2vec

训练词向量的模型，有连续词袋模型和跳词模型

连续词袋模型(CBOW)

我们有一个词表WW，训练集为大量的句子，对于某个句子w1…wmw_{1}\dots w_{m}，我们采用如下的方式进行训练：

  • 在句中任选一位置合适的词wtw_{t}
  • 取其前后各cc个词的词向量进行求和并激活：xw=g(∑i=1c(wt−i+wt+i))x_{w} = g(\sum\limits_{i=1}^{c}(w_{t-i} + w_{t + i}))
  • 将xwx_{w}作为输入传给一个霍夫曼树，其中每一个内部节点是一个神经元，叶节点为所有的词
  • 霍夫曼树的内部节点，输入为一个词，输出为选择左边或者右边的概率，最终我们要极大到达原来的词wtw_{t}的概率，也即神经网络需要训练每个节点的参数使得root→wt\mathrm{root}\rightarrow w_{t}这条路径的概率尽可能大

跳词模型

PPT没说，略

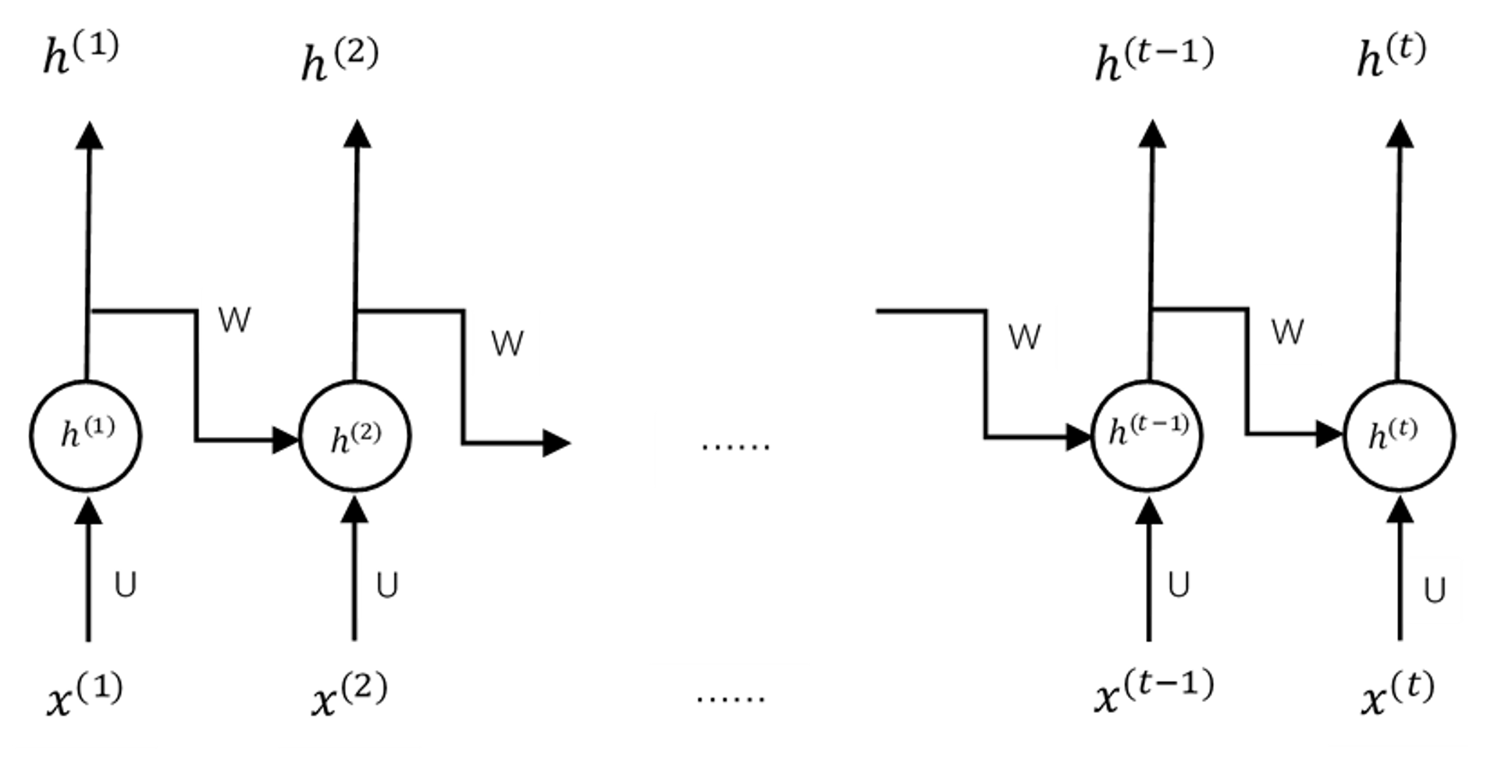
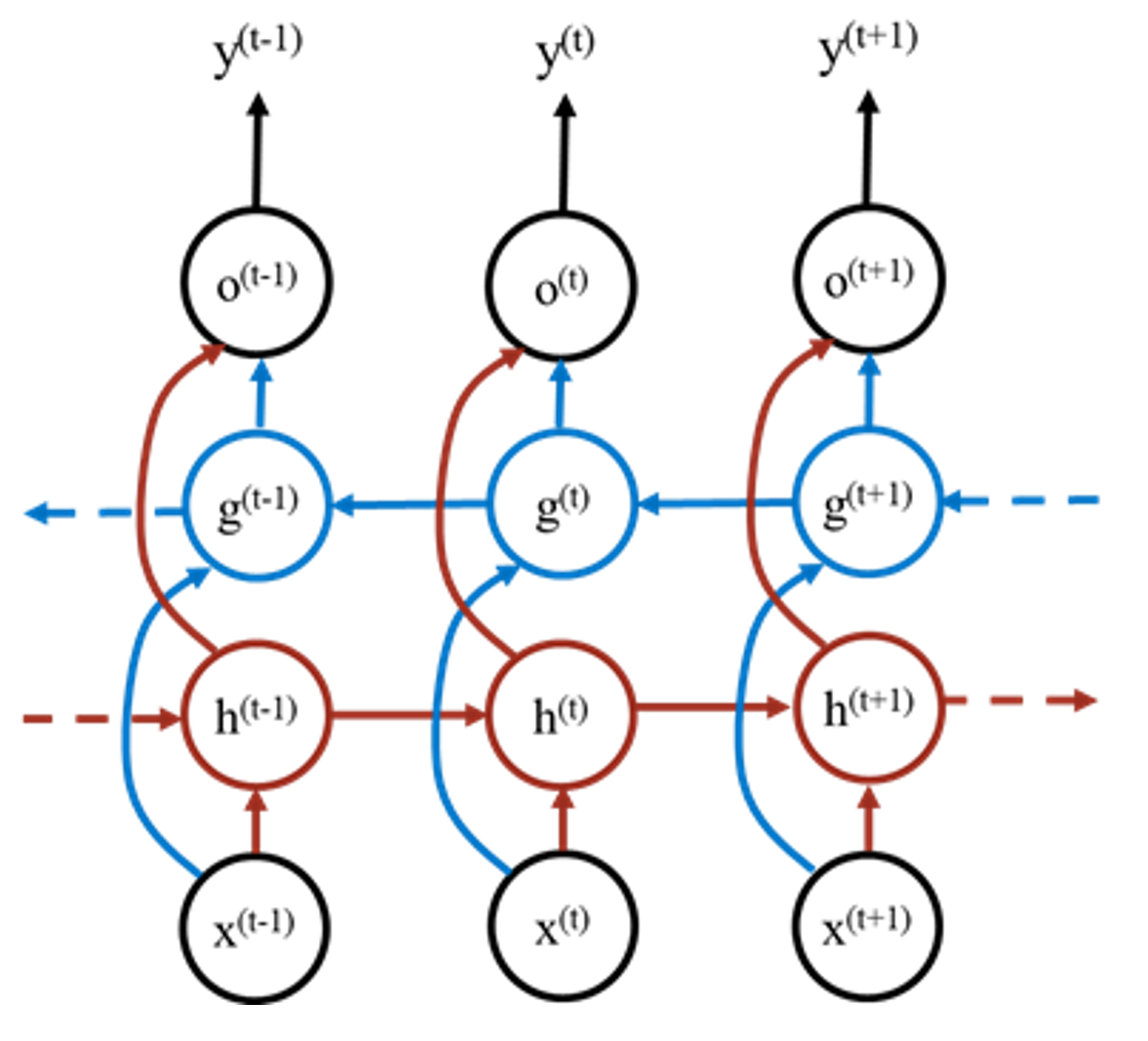
循环神经网络RNN

循环神经网络
循环神经网络

如上图，我们利用输入来更新状态向量h(k)=[h1(k),…,hm(k)]h^{(k)} = [h_{1}^{(k)}, \dots, h_{m}^{(k)}]

最终输出的处理方式根据相应的实际问题变化而变化，例如情感分类问题可以接一个全连接层与一个softmax

并且我们可以将每一次循环的结果都输出出来进行相应的处理，例如看图说话的过程可以将每一次循环的结果分别做一次全连接与softmax来作为一个字，最终组成一段话

双向循环神经网络

由于一些情况下序列不仅是有正向的关系，利于一句话的某个词需要根据上下文而不是上文才能确定，而采用传统的RNN会导致下文信息的丢失，因此采用一个双向的形式

双向循环神经网络
双向循环神经网络

如上图，这样可以同时考虑上下文的信息

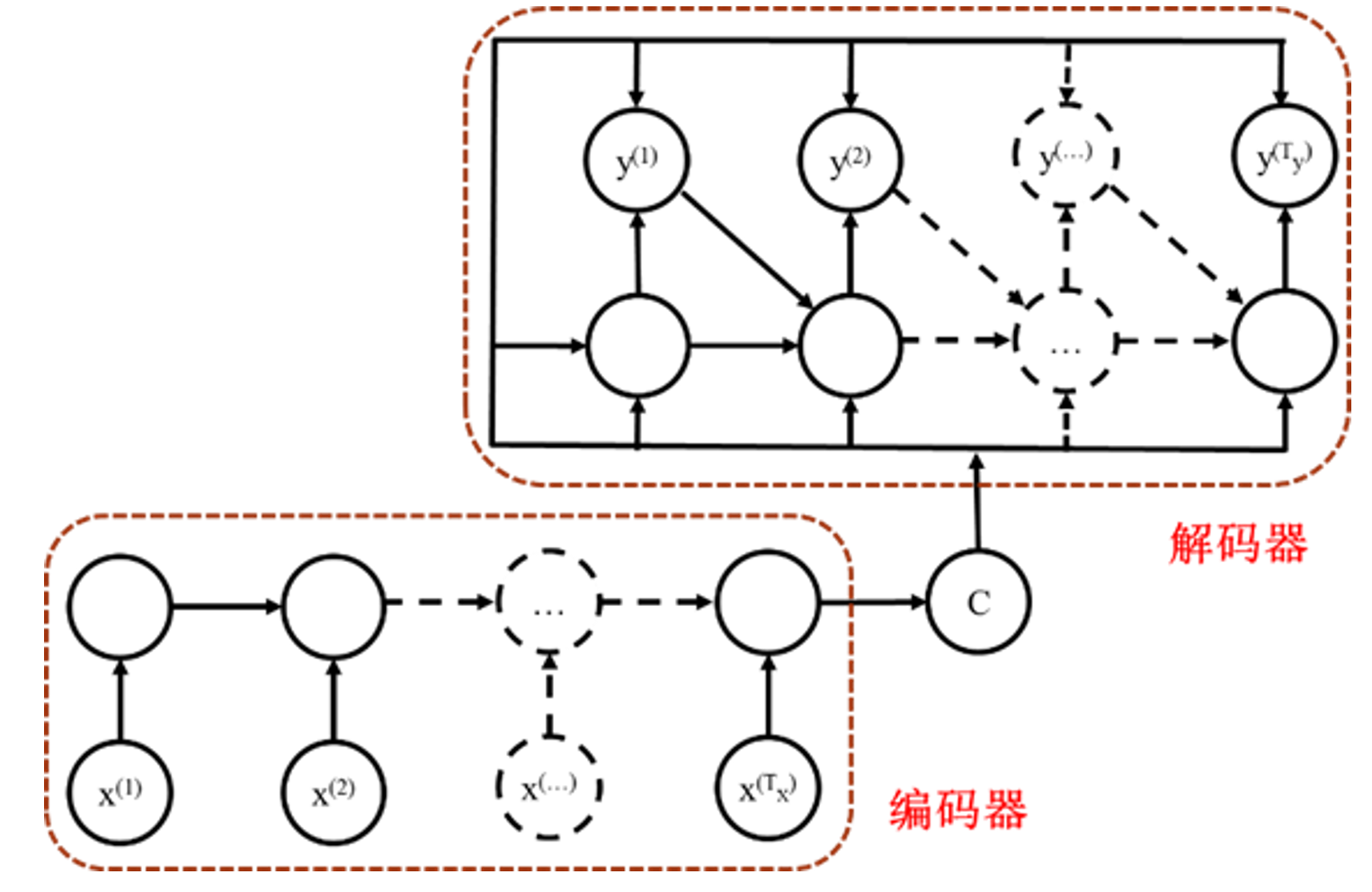
序列到序列

考虑在实际中，许多问题的输入也是一个序列而不是一个简单的向量或矩阵，例如问答、翻译等，因此采用序列到序列的RNN模式，即采用编码器-解码器模块，现将输入序列编码为矩阵或向量，再将其放入解码器中

序列到序列循环神经网络
序列到序列循环神经网络

长短期记忆网络LSTM

简单RNN的问题：

  • 长期依赖：如果输入序列具有距离较远的依赖关系，那RNN很容易丢失这层关系，例如"bei jing shi yi ge mei li de"这句话，"shi"具体的字的确认就很困难，需要根据后续的输入来确定，而这层关系被短期的RNN丢弃
  • 重点选择问题：序列中不同部分的重要性不同
  • 梯度消失问题

因此改进为LSTM

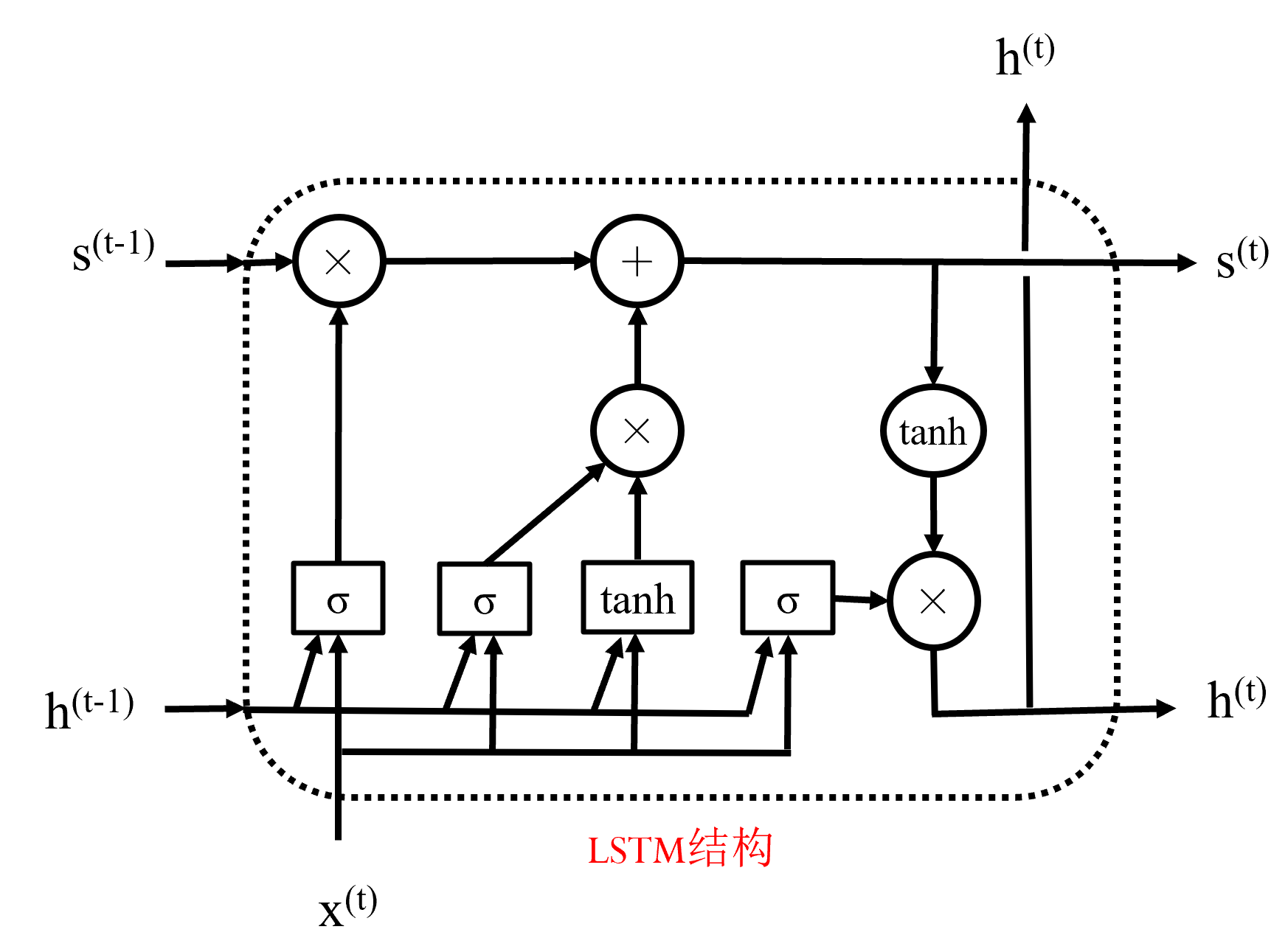
LSTM循环结构
LSTM循环结构

在上图的循环结构中，维护两个状态ss与hh，循环结构内部是由“门”组成的

门是指一层神经网络，例如σ\sigma门就指的是将输入接一个全连接层和一个σ\sigma激活函数作为输出，全连接层的作用是将输入维数与状态的维数进行匹配

结构中×\times等算数运算符代表的是按位操作，相当于是对原有数据进行重新加权与筛选

下面依次介绍上图中的门

遗忘门

左数第一个，为σ\sigma门，将原有状态h(t−1)h^{(t-1)}和输入共同作为输入，经过全连接与σ\sigma之后直接与状态向量s(t−1)s^{(t-1)}按位相乘

表示遗忘掉状态中的一些信息，防止过拟合

输入部分

  • 输入门：左数第二个，也为σ\sigma门
  • 输入处理单元：左数第三个，为tanh⁡\tanh门

将这两个门的处理结果按位乘，表示这一轮学到的东西，之后与遗忘后的状态向量s′(t−1)s^{'(t-1)}按位加，完成学习的过程得到s(t)s^{(t)}

输出部分

  • 输出门：左数第四个，为σ\sigma门
  • 输出处理单元：不是门！是一个单独的tanh⁡\tanh函数

将这两个的处理结果按位乘得到新一轮的输出状态h(t)h^{(t)}

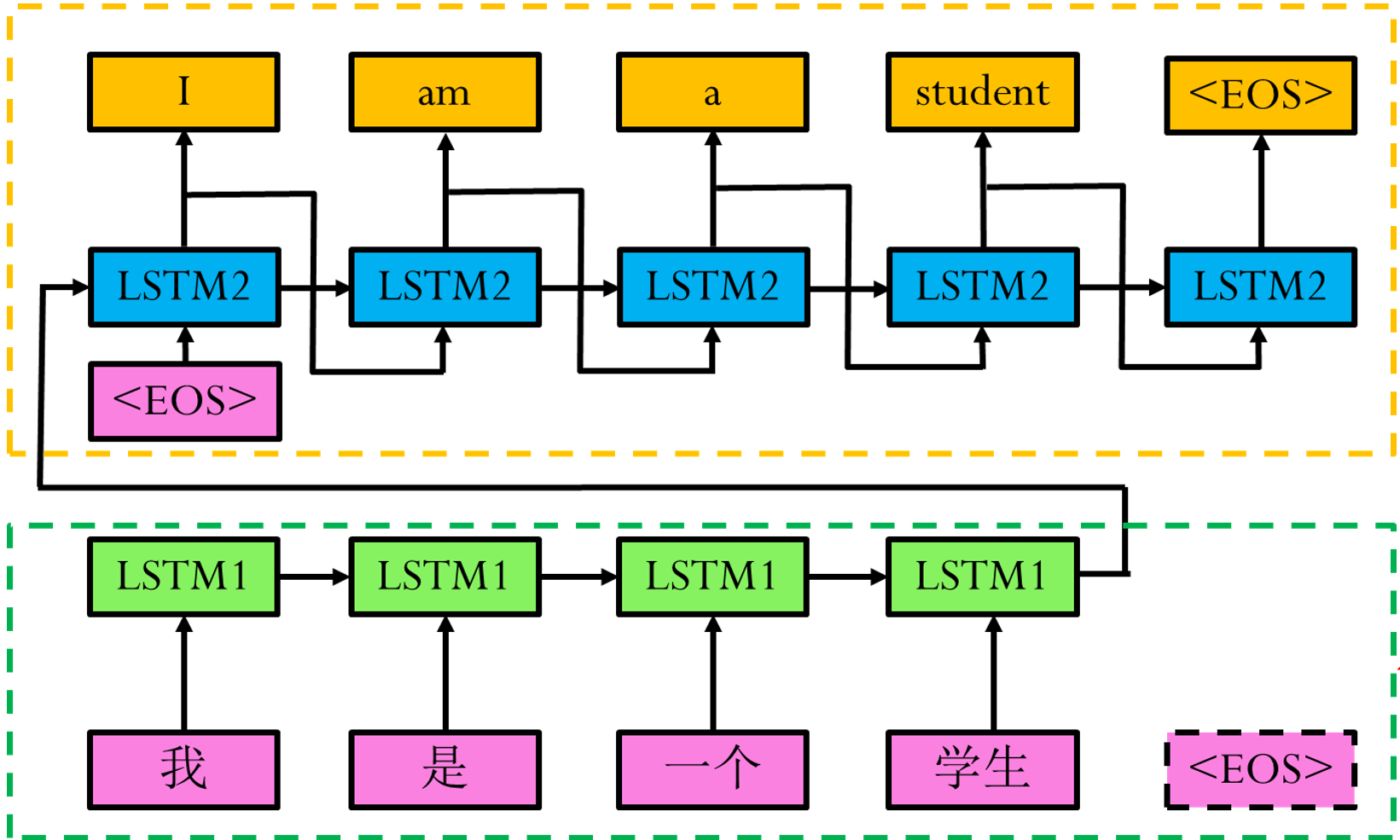
实例

利用LSTM解决序列到序列的问题

编码器-解码器模式的LSTM
编码器-解码器模式的LSTM
许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。