人智导 对抗搜索

对抗搜索

对于一些分支极多的对抗式问题，穷举法所需要消耗的时间、空间资源无法承受，无法实现，因此考虑充分的剪枝

极小-极大模型

进行有限步内的穷举，从根节点出发，叶节点标记得分，并且期望每位选手都选择对于自己最有利的走法，最后选择期望得分最高的一步

极大-极小模型示例图

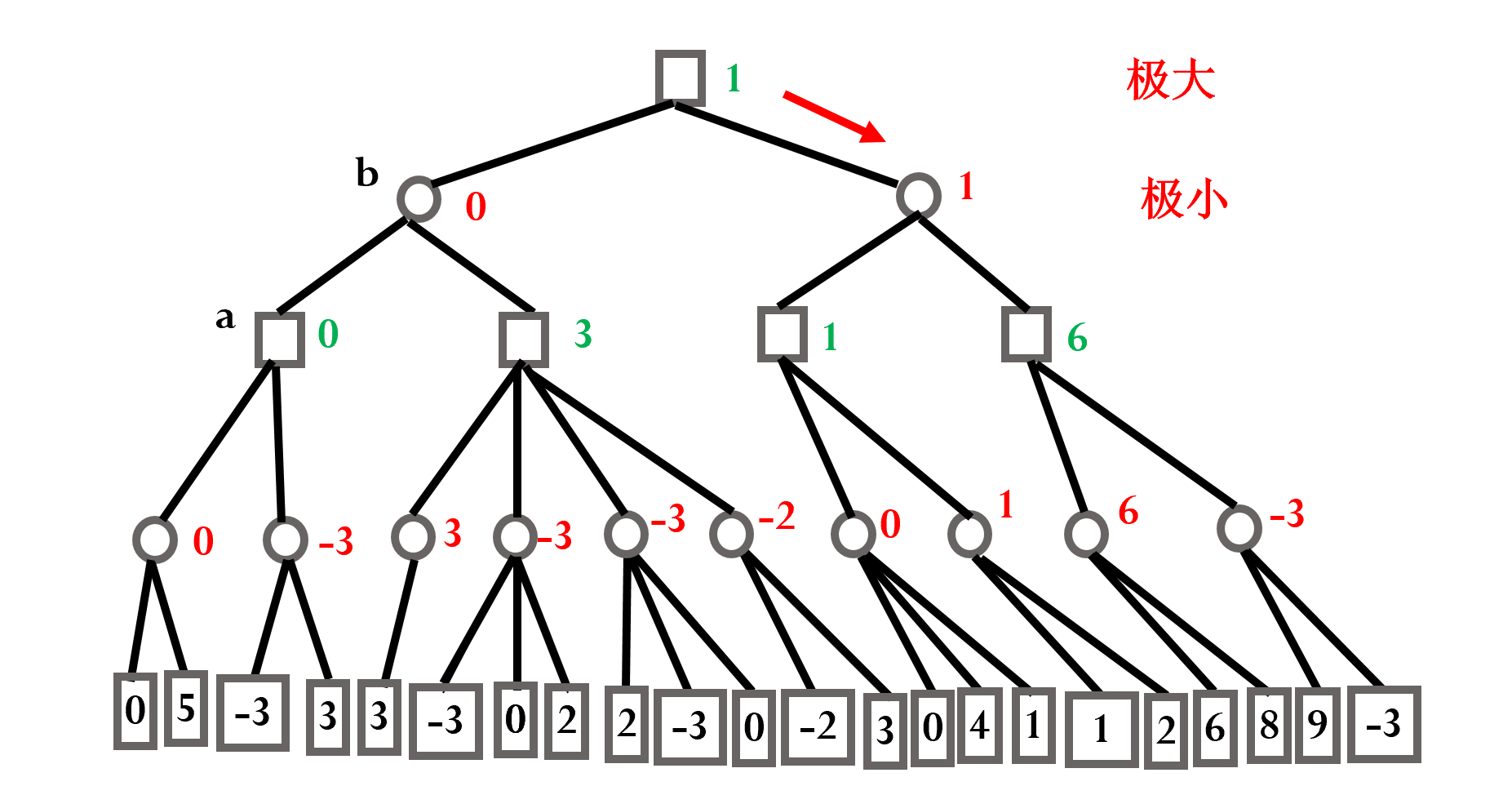
图中，两种图形代表两位选手，分别记为$A, B$，叶节点上所标记的为$A$在四步之后的期望得分，每位选手每步都是期望自身得分尽量高（对方得分尽量低）

但是极小极大仍然没有剪枝，时空资源仍然无法承受

α-β剪枝算法

$\alpha$-$\beta$ 剪枝算法如下

实例如下：注意比较时需要和祖先节点而不是父节点比较

alpha-beta剪枝实例

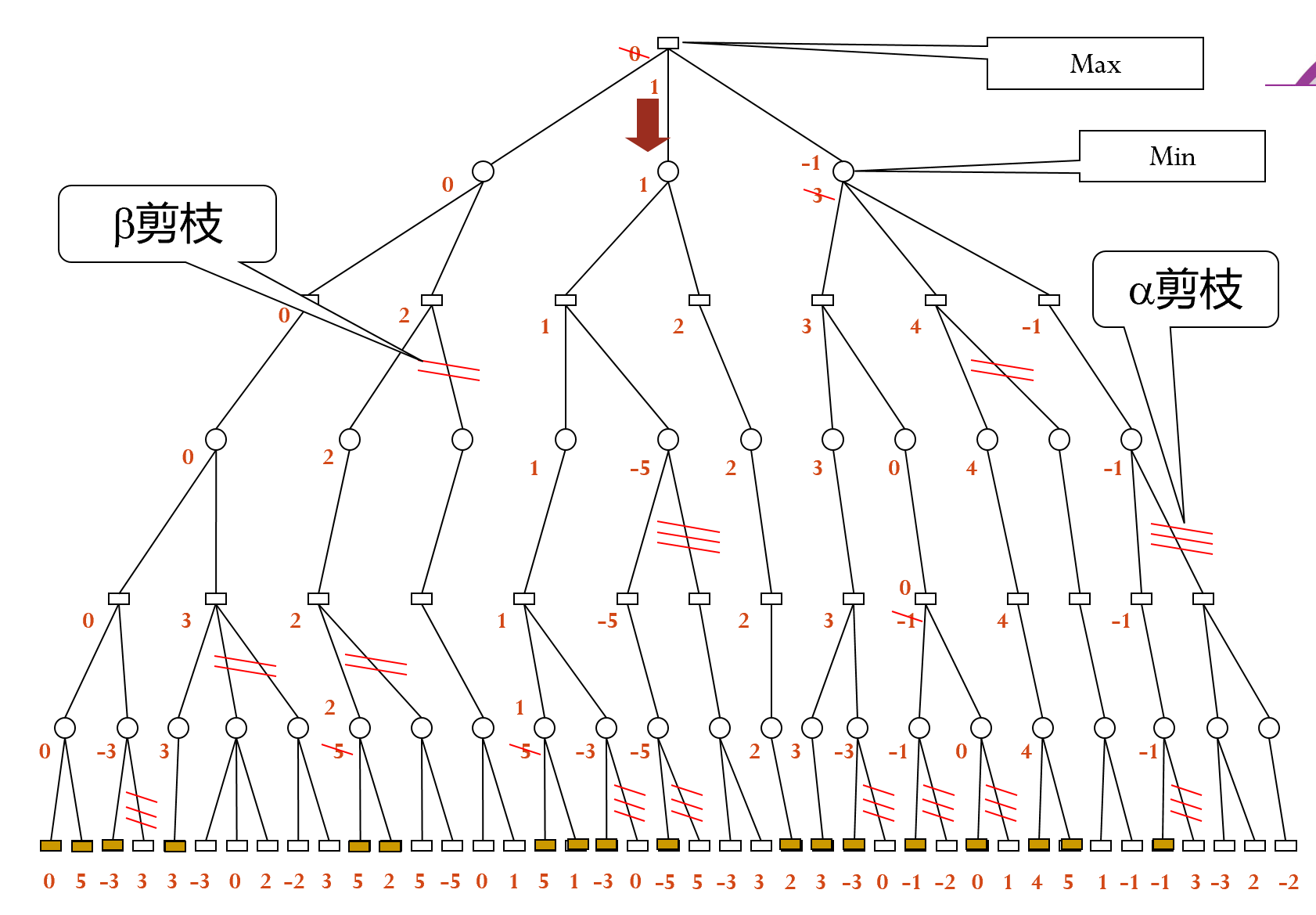
每次$\alpha$-$\beta$ 剪枝只能得到下一步的走法

蒙特卡洛(MCTS)

基本思想：

• 可能出现的状态用状态树表示
• 逐步扩展树节点
• 父节点利用子节点的结果
• 随时得到行为评价

基本过程为：

选择策略

考虑两方面因素：

• 充分探索尚未探索的节点
• 利用效果尽量好的节点

因此采用多臂老虎机模型

采用信心上限算法：每次选择信心上限最大的节点，节点$j$的信心上限计算方式为：

$$I_{j} = \overline{X}_{j} + c\sqrt{\frac{2\ln(n)}{T_{j}(n)}}$$

其中参数含义为：

• $c$：调节参数
• $n$：访问次数
• $T_{j}(n)$：此时节点 $j$ 被访问的次数
• $\overline{X}_{j}$：此时节点 $j$ 的平均收益

以围棋为例，每一次模拟可以看成是随机落点，平均收益可以看成是胜率，如下图，其中为简便令$c = 0$，最终选择根节点的子节点中胜率最大的节点作为下一步：

采用UBC选择的MCTS

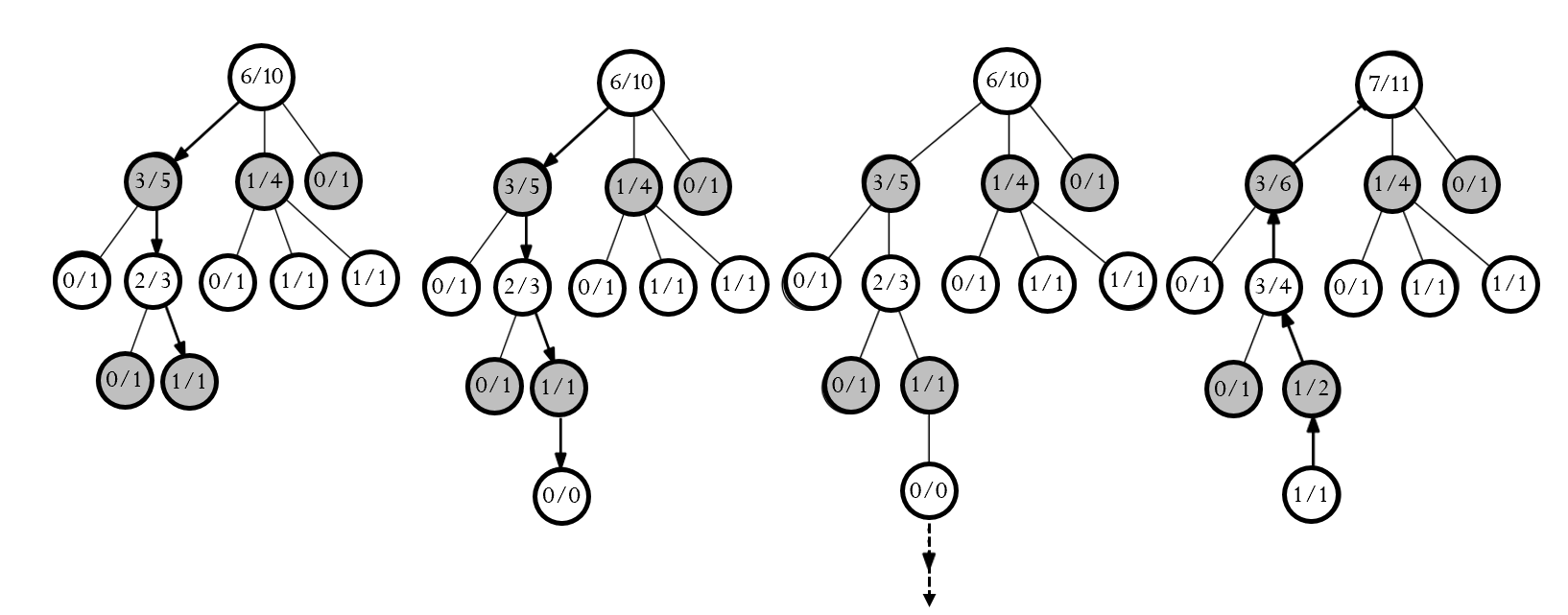
注意：

AlphaGo

为了解决MCTS的盲目性问题（随机落子），将神经网络与蒙特卡洛结合起来，使用了策略网络与估值网络两种神经网络

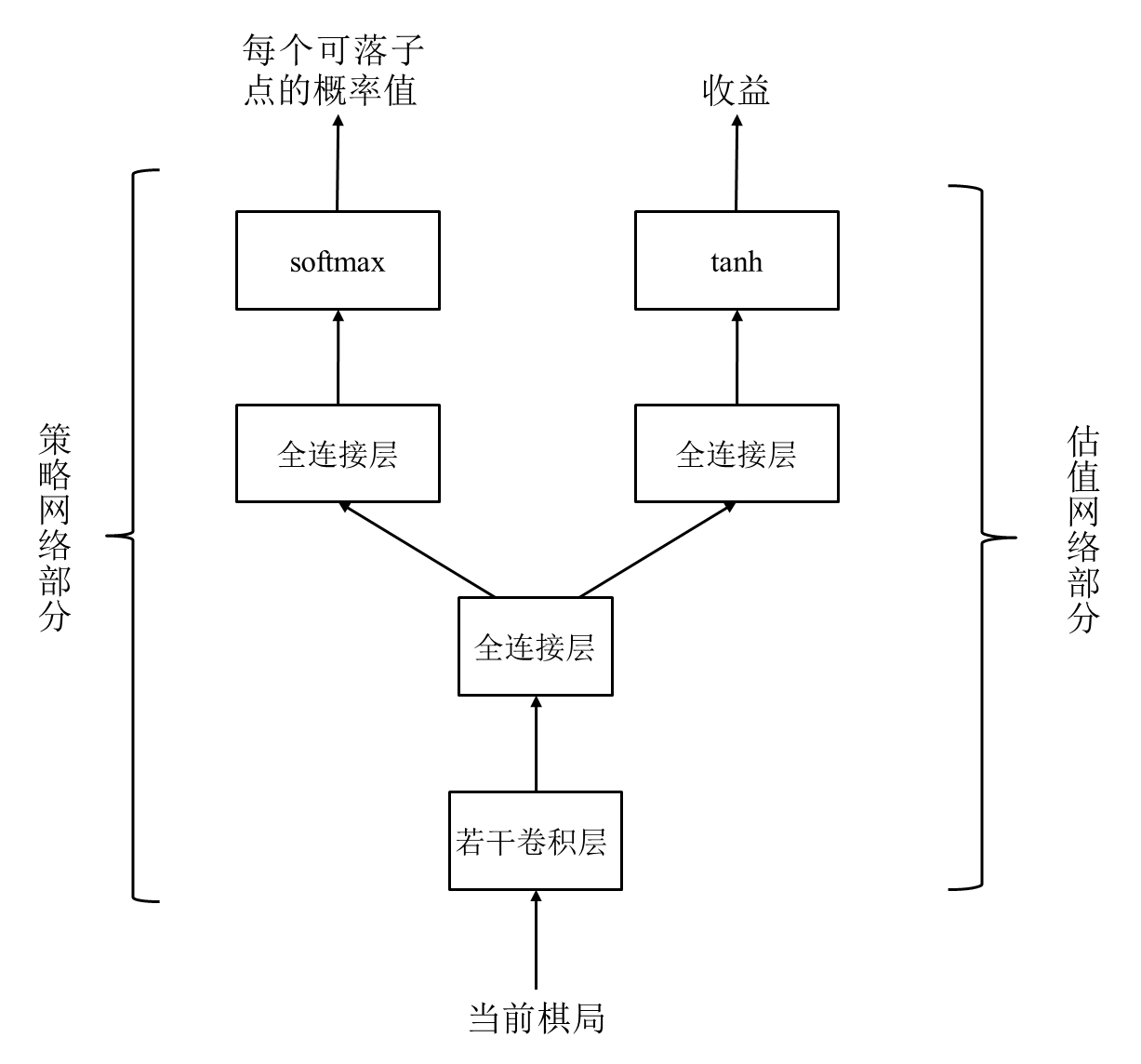
策略网络

一个神经网络，用于提供行棋概率

策略网络

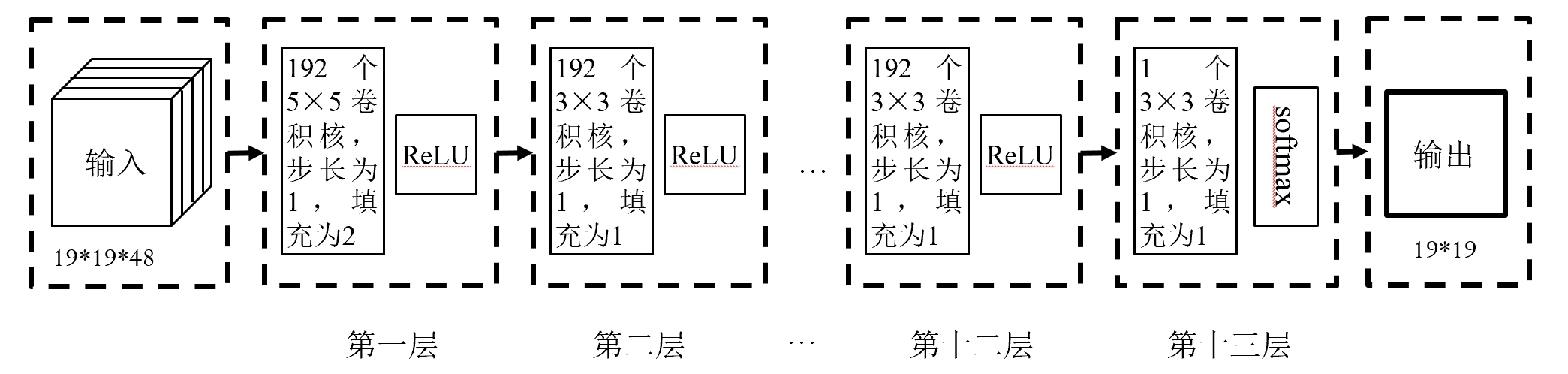
策略网络可以看成是一个361类别分类问题，通过人类棋手的棋谱进行训练，损失函数为

$$L(w) = -t_{a}\log(p_{a})$$

其中$t_{a}$为实际落子概率，$p_{a}$为网络落子概率

估值网络

一个神经网络，用于提供棋局收益

估值网络

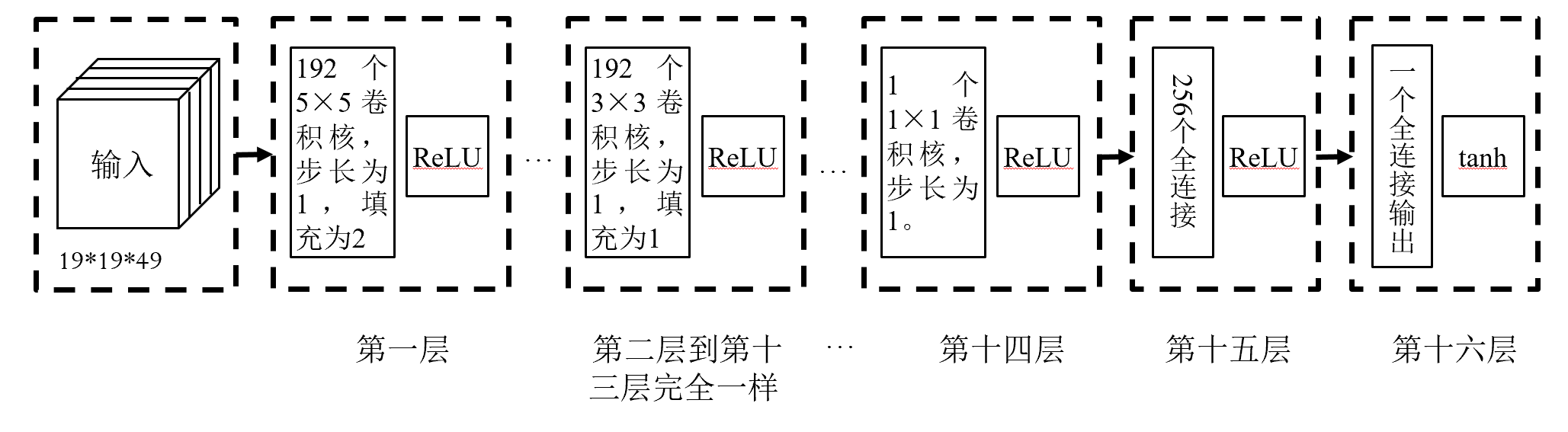
估值网络可以看成回归问题，也是通过人类棋手棋谱进行训练，损失函数：

$$L(w) = (R - V(s))^{2}$$

其中$R$为实际收益，$1$ 胜 $-1$ 负，$V(s)$为网络输出

与MCTS融合

给定参数 $\lambda$

每次模拟收益为：

$$v_{i}(s) = \lambda \text{value}(s) + (1 - \lambda)\text{sim}(s)$$

其中 $\text{value}(s)$ 为估值网络输出，$\text{sim}(s)$ 为模拟结果

因此定义平均收益：

$$Q(s_{a}) = \frac{\sum\limits_{i=1}^{n}v_{i}(s_{a})}{n}$$

定义探索项：

$$u(s_{a}) = c \cdot p(s_{a})\frac{\sqrt{N(s)}}{N(s_{a}) + 1}$$

其中：

• $s_{a}$代表棋局$s$在$a$处落子后的棋局
• $N(s)$代表对于棋局$s$的模拟次数
• $p(s)$代表策略网络对于$s$的输出
• $c$为系数

信心上限切换为：

MCTS过程如下：

• 信息：每个节点记录收益、到达该节点概率与被选择次数
• 选择：从根节点开始，每次选择子节点中信心上限最大的节点，直到叶节点即停止并选中
• 生成：生成选中节点的所有叶节点（也即所有可能的落子），并规定了最大的节点深度
• 模拟：采用推演策略网络（更快），计算其$v_{i}$
• 回传：注意正负号（即注意行棋是双方依次进行）

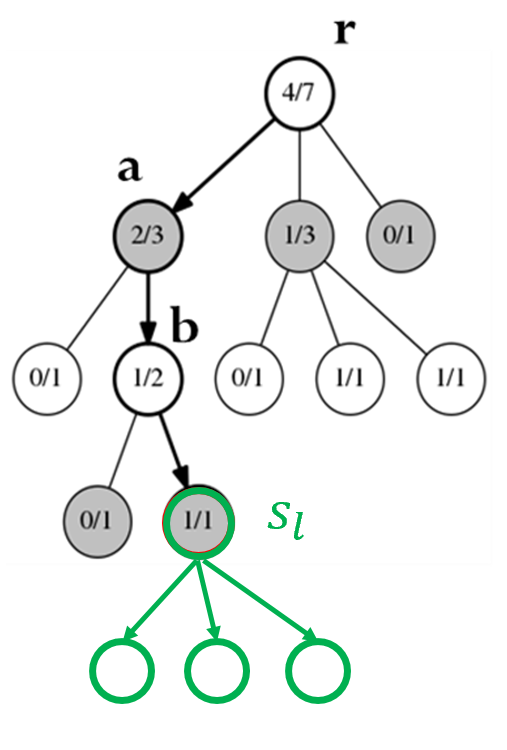
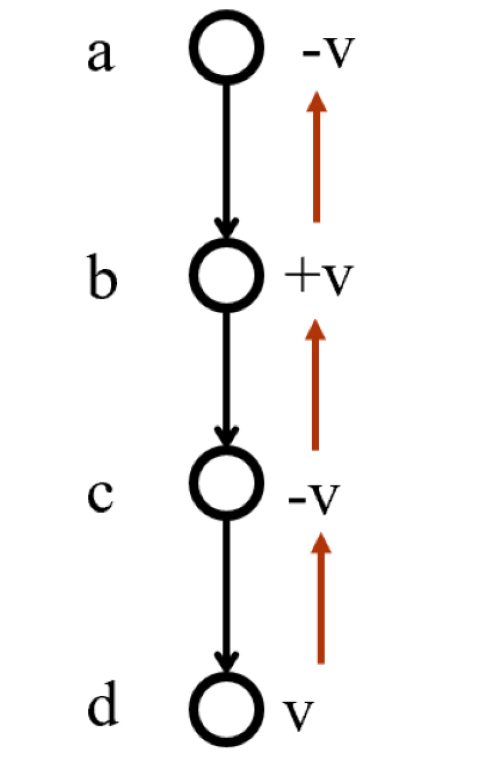
最终将根节点的子节点中，被选择次数最多的节点作为选择

深度强化学习方法

以围棋为例，通过自己博弈训练策略网络，三种实现方法：

1. 策略梯度：学习每个点获胜的概率
2. 价值评估：学习每个点获得最大收益的概率
3. 演员评价方法：学习到每个落子点获得最大收益增量的概率

策略梯度

数据由自我博弈产生，损失函数为：

$$L(w) = - t_{a}\log(p_{a})$$

其中，$p_{a}$为当前棋局在$a$处下棋的概率，$t_{a}\in\{-1, 1\}$为胜负值

基于策略梯度的强化学习流程

注意点：

1. 强化学习过程中，每个样本只使用一次
2. 该方法学习到的是每个可落子点行棋的获胜概率

价值评估

输入为当前棋局和行棋点，输出为该行棋点的价值，在$[-1, 1]$之间，数据也是自我博弈产生，损失函数为：

$$L(w) = (R - V(s, a))^{2}$$

其中，$R$为胜负值，$V(s, a)$为棋局$s$在$a$处落子后网络的输出

演员-评价方法

利用收益增量评价一步棋的好坏：

$$A = Q(s, a) - V(s)$$

其中，$V(s)\in[-1, 1]$为棋局$s$的预期收益，$Q(s, a)\in[-1, 1]$为$s$在$a$处行棋之后的收益，在实际中常去$Q(s, a) = R$为胜负值，最终$A$越大收益越好

演员-策略网络，评价-估值网络

损失函数为：

$$\begin{align*} L(w) &= L_{1}(w) + \lambda L_{2}(w) \\ &= A^{2} - \lambda A\log(p_{a}) \end{align*}$$

AlphaGo Zreo

将估值网络和策略网络合并为“双输出”网络

Alpha-Zero原理

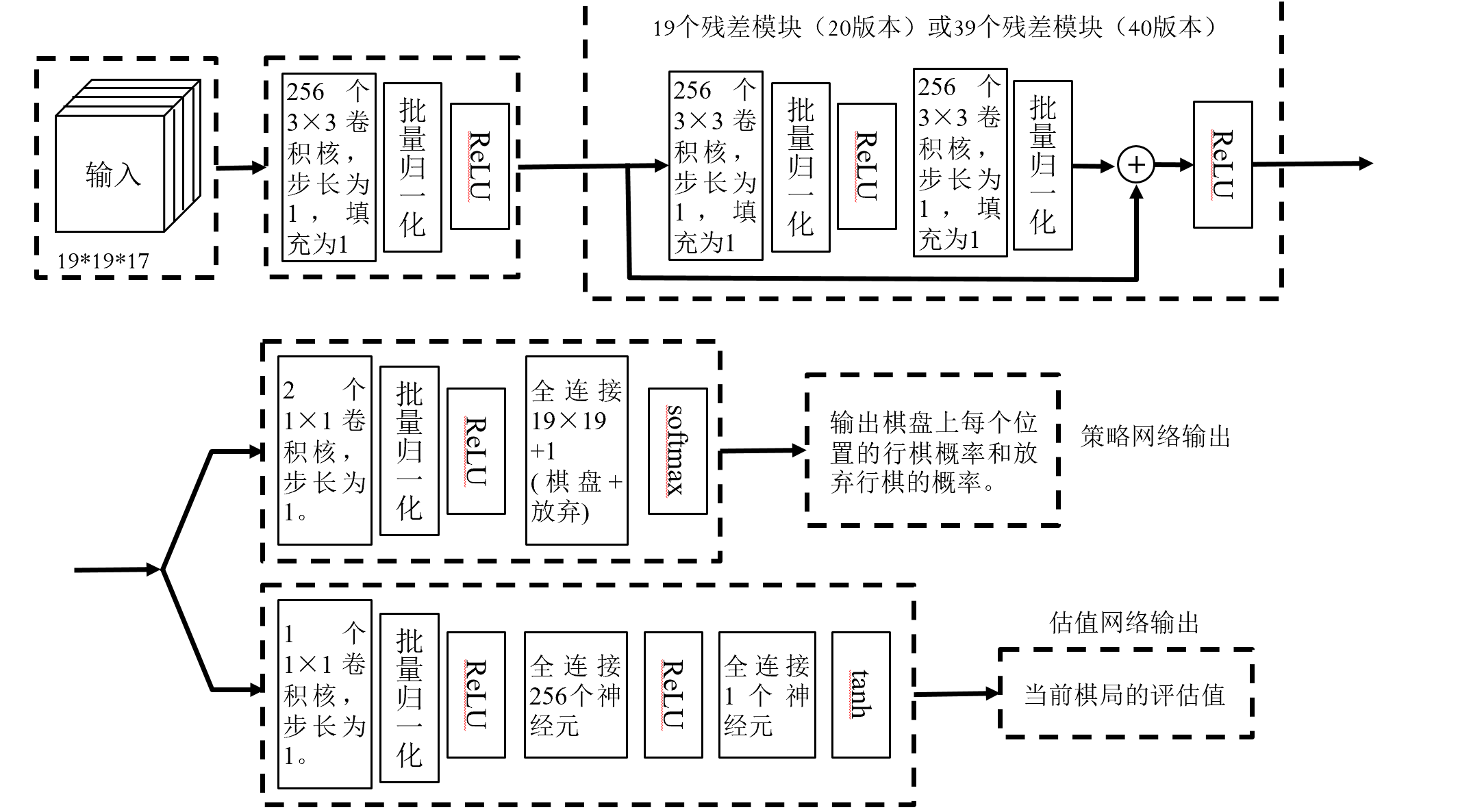
与MCTS融合

与AlphaGo基本相同，差别如下：

1. 模拟被估值网络完全取代，模拟收益$v_{i}(s)$即为估值网络的输出
2. 规定了总模拟次数

结合MCTS与深度强化学习

Alpha-Zero中的深度强化学习

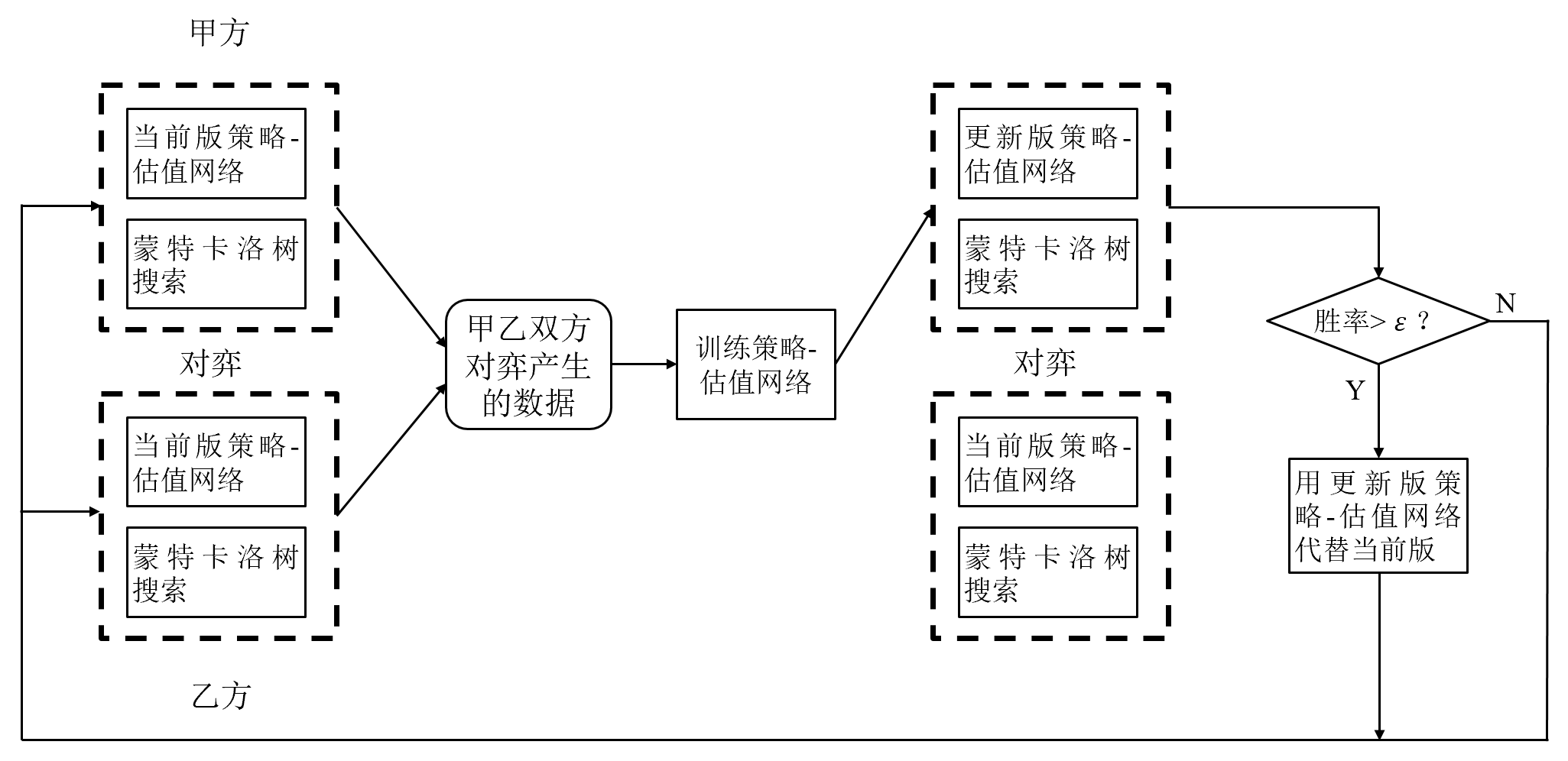
损失函数为：

$$\begin{align*} L_{value} &= (R - v)^{2} \\ L_{strategy} &= -\sum\limits_{i=1}^{362}\pi_{i}\log(p_{i}) \\ L &= L_{value} + L_{strategy} + ||\theta||^{2} \end{align*}$$

其中$R$为胜负值，$v$为估值网络输出，$\pi_{i}$为MCTS给出的该走法概率，$p_{i}$为策略网络给出的该走法概率

引入多样性

人为引入噪声，增加策略网络输出的随机性，通常增加一个狄利克雷分布，生成一些大多值为0，小部分值较大的随机变量，并修正策略网络输出为：

$$p \Leftarrow \lambda p + (1 - \lambda) p_{d}$$